Near-optimality for infinite-horizon restless bandits with many arms

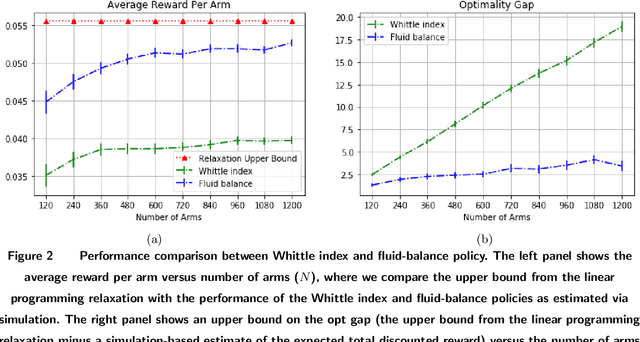
Restless bandits are an important class of problems with applications in recommender systems, active learning, revenue management and other areas. We consider infinite-horizon discounted restless bandits with many arms where a fixed proportion of arms may be pulled in each period and where arms share a finite state space. Although an average-case-optimal policy can be computed via stochastic dynamic programming, the computation required grows exponentially with the number of arms $N$. Thus, it is important to find scalable policies that can be computed efficiently for large $N$ and that are near optimal in this regime, in the sense that the optimality gap (i.e. the loss of expected performance against an optimal policy) per arm vanishes for large $N$. However, the most popular approach, the Whittle index, requires a hard-to-verify indexability condition to be well-defined and another hard-to-verify condition to guarantee a $o(N)$ optimality gap. We present a method resolving these difficulties. By replacing a global Lagrange multiplier used by the Whittle index with a sequence of Lagrangian multipliers, one per time period up to a finite truncation point, we derive a class of policies, called fluid-balance policies, that have a $O(\sqrt{N})$ optimality gap. Unlike the Whittle index, fluid-balance policies do not require indexability to be well-defined and their $O(\sqrt{N})$ optimality gap bound holds universally without sufficient conditions. We also demonstrate empirically that fluid-balance policies provide state-of-the-art performance on specific problems.