Weakly Coupled Deep Q-Networks
Paper and Code
Oct 28, 2023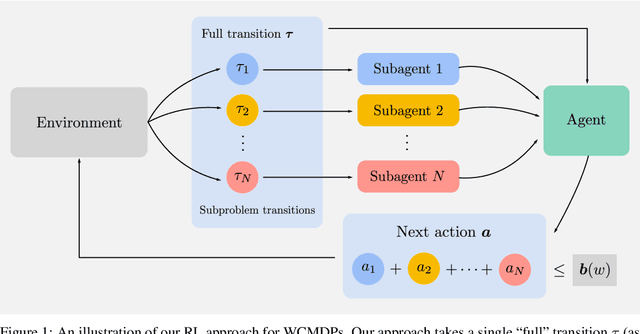

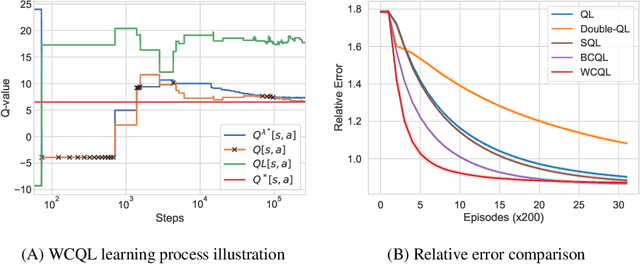
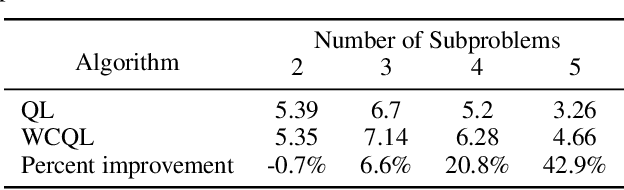
We propose weakly coupled deep Q-networks (WCDQN), a novel deep reinforcement learning algorithm that enhances performance in a class of structured problems called weakly coupled Markov decision processes (WCMDP). WCMDPs consist of multiple independent subproblems connected by an action space constraint, which is a structural property that frequently emerges in practice. Despite this appealing structure, WCMDPs quickly become intractable as the number of subproblems grows. WCDQN employs a single network to train multiple DQN "subagents", one for each subproblem, and then combine their solutions to establish an upper bound on the optimal action value. This guides the main DQN agent towards optimality. We show that the tabular version, weakly coupled Q-learning (WCQL), converges almost surely to the optimal action value. Numerical experiments show faster convergence compared to DQN and related techniques in settings with as many as 10 subproblems, $3^{10}$ total actions, and a continuous state space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge