Sparse Autoencoders Do Not Find Canonical Units of Analysis

A common goal of mechanistic interpretability is to decompose the activations of neural networks into features: interpretable properties of the input computed by the model. Sparse autoencoders (SAEs) are a popular method for finding these features in LLMs, and it has been postulated that they can be used to find a \textit{canonical} set of units: a unique and complete list of atomic features. We cast doubt on this belief using two novel techniques: SAE stitching to show they are incomplete, and meta-SAEs to show they are not atomic. SAE stitching involves inserting or swapping latents from a larger SAE into a smaller one. Latents from the larger SAE can be divided into two categories: \emph{novel latents}, which improve performance when added to the smaller SAE, indicating they capture novel information, and \emph{reconstruction latents}, which can replace corresponding latents in the smaller SAE that have similar behavior. The existence of novel features indicates incompleteness of smaller SAEs. Using meta-SAEs -- SAEs trained on the decoder matrix of another SAE -- we find that latents in SAEs often decompose into combinations of latents from a smaller SAE, showing that larger SAE latents are not atomic. The resulting decompositions are often interpretable; e.g. a latent representing ``Einstein'' decomposes into ``scientist'', ``Germany'', and ``famous person''. Even if SAEs do not find canonical units of analysis, they may still be useful tools. We suggest that future research should either pursue different approaches for identifying such units, or pragmatically choose the SAE size suited to their task. We provide an interactive dashboard to explore meta-SAEs: https://metasaes.streamlit.app/

Efficient computation of the Knowledge Gradient for Bayesian Optimization

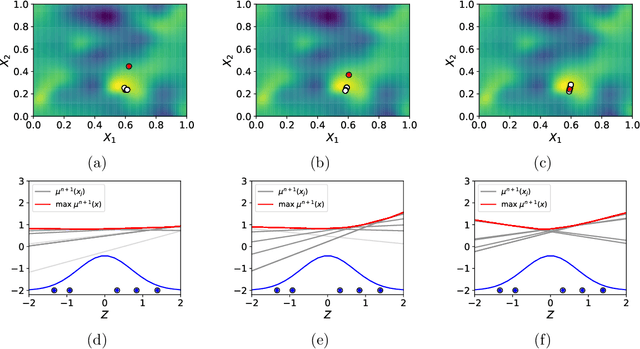
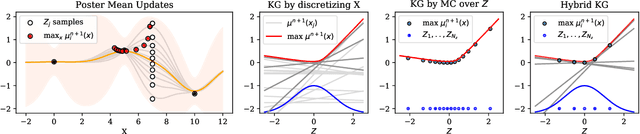
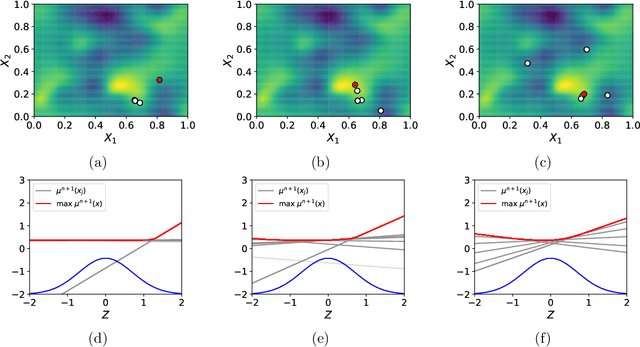
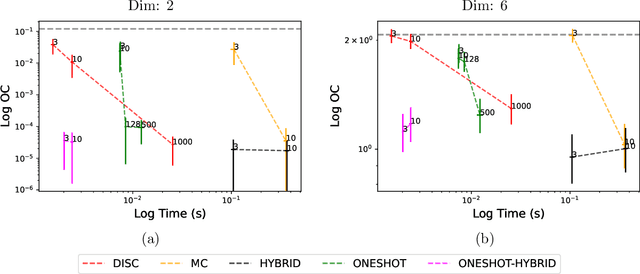
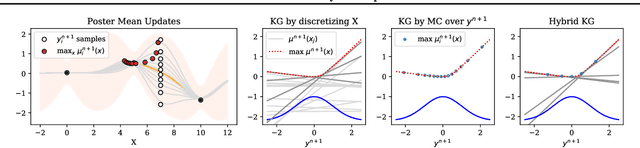
Bayesian optimization is a powerful collection of methods for optimizing stochastic expensive black box functions. One key component of a Bayesian optimization algorithm is the acquisition function that determines which solution should be evaluated in every iteration. A popular and very effective choice is the Knowledge Gradient acquisition function, however there is no analytical way to compute it. Several different implementations make different approximations. In this paper, we review and compare the spectrum of Knowledge Gradient implementations and propose One-shot Hybrid KG, a new approach that combines several of the previously proposed ideas and is cheap to compute as well as powerful and efficient. We prove the new method preserves theoretical properties of previous methods and empirically show the drastically reduced computational overhead with equal or improved performance. All experiments are implemented in BOTorch and code is available on github.

A Unified Statistical Learning Model for Rankings and Scores with Application to Grant Panel Review

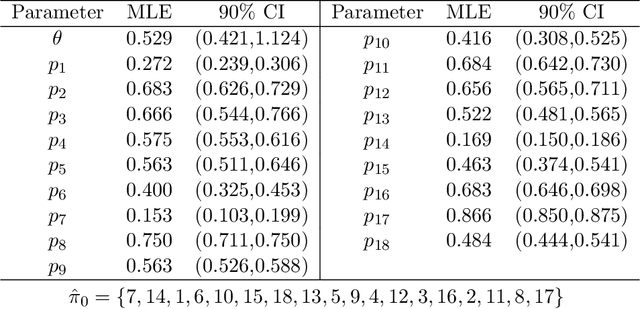
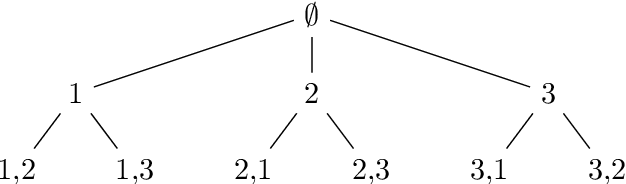
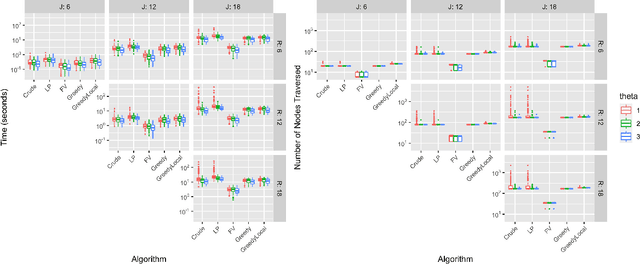
Rankings and scores are two common data types used by judges to express preferences and/or perceptions of quality in a collection of objects. Numerous models exist to study data of each type separately, but no unified statistical model captures both data types simultaneously without first performing data conversion. We propose the Mallows-Binomial model to close this gap, which combines a Mallows' $\phi$ ranking model with Binomial score models through shared parameters that quantify object quality, a consensus ranking, and the level of consensus between judges. We propose an efficient tree-search algorithm to calculate the exact MLE of model parameters, study statistical properties of the model both analytically and through simulation, and apply our model to real data from an instance of grant panel review that collected both scores and partial rankings. Furthermore, we demonstrate how model outputs can be used to rank objects with confidence. The proposed model is shown to sensibly combine information from both scores and rankings to quantify object quality and measure consensus with appropriate levels of statistical uncertainty.

Factorized Gaussian Process Variational Autoencoders

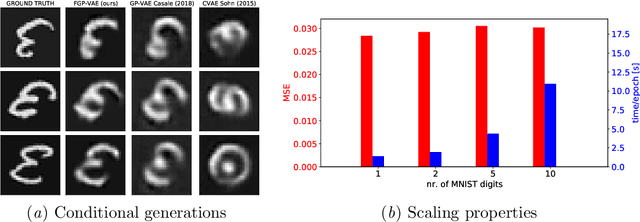
Variational autoencoders often assume isotropic Gaussian priors and mean-field posteriors, hence do not exploit structure in scenarios where we may expect similarity or consistency across latent variables. Gaussian process variational autoencoders alleviate this problem through the use of a latent Gaussian process, but lead to a cubic inference time complexity. We propose a more scalable extension of these models by leveraging the independence of the auxiliary features, which is present in many datasets. Our model factorizes the latent kernel across these features in different dimensions, leading to a significant speed-up (in theory and practice), while empirically performing comparably to existing non-scalable approaches. Moreover, our approach allows for additional modeling of global latent information and for more general extrapolation to unseen input combinations.

Scalable Gaussian Process Variational Autoencoders

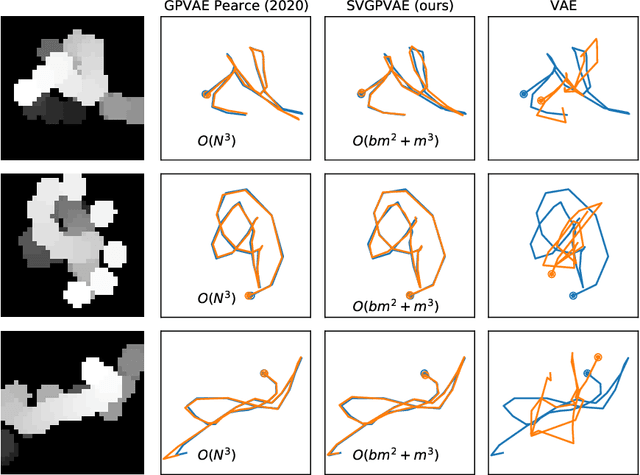
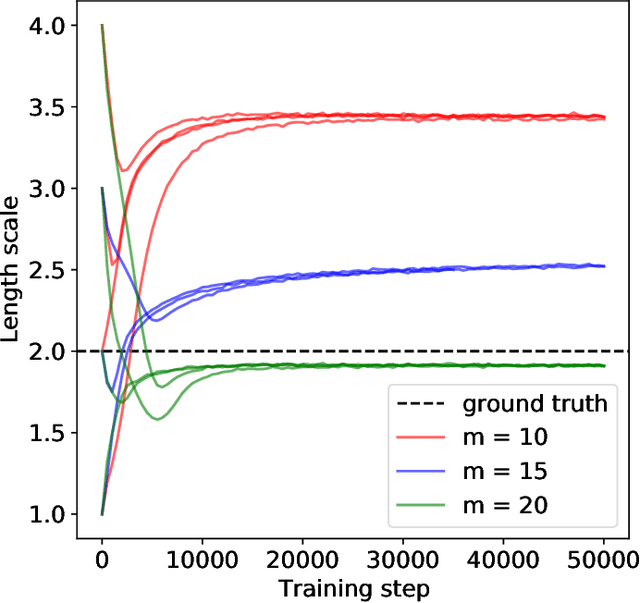
Conventional variational autoencoders fail in modeling correlations between data points due to their use of factorized priors. Amortized Gaussian process inference through GP-VAEs has led to significant improvements in this regard, but is still inhibited by the intrinsic complexity of exact GP inference. We improve the scalability of these methods through principled sparse inference approaches. We propose a new scalable GP-VAE model that outperforms existing approaches in terms of runtime and memory footprint, is easy to implement, and allows for joint end-to-end optimization of all components.

Sparse Gaussian Process Variational Autoencoders

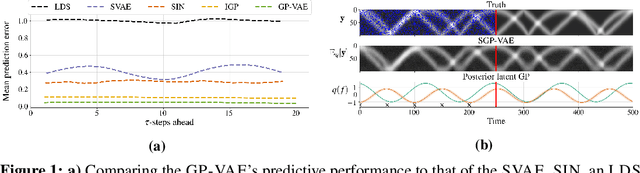
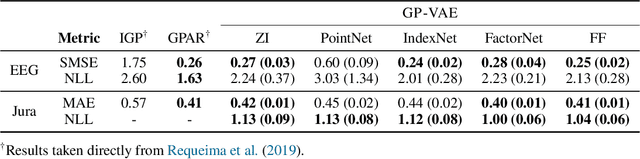
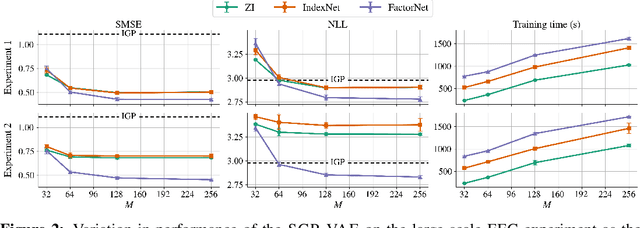
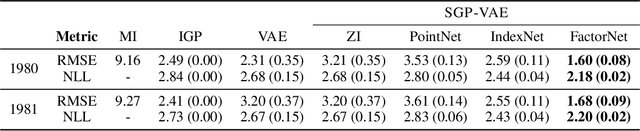
Large, multi-dimensional spatio-temporal datasets are omnipresent in modern science and engineering. An effective framework for handling such data are Gaussian process deep generative models (GP-DGMs), which employ GP priors over the latent variables of DGMs. Existing approaches for performing inference in GP-DGMs do not support sparse GP approximations based on inducing points, which are essential for the computational efficiency of GPs, nor do they handle missing data -- a natural occurrence in many spatio-temporal datasets -- in a principled manner. We address these shortcomings with the development of the sparse Gaussian process variational autoencoder (SGP-VAE), characterised by the use of partial inference networks for parameterising sparse GP approximations. Leveraging the benefits of amortised variational inference, the SGP-VAE enables inference in multi-output sparse GPs on previously unobserved data with no additional training. The SGP-VAE is evaluated in a variety of experiments where it outperforms alternative approaches including multi-output GPs and structured VAEs.

Bayesian Optimisation vs. Input Uncertainty Reduction

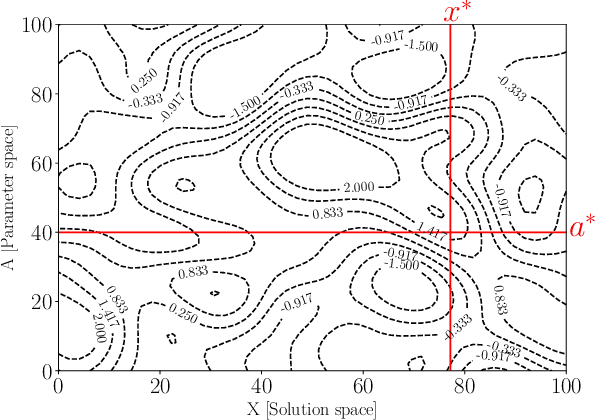
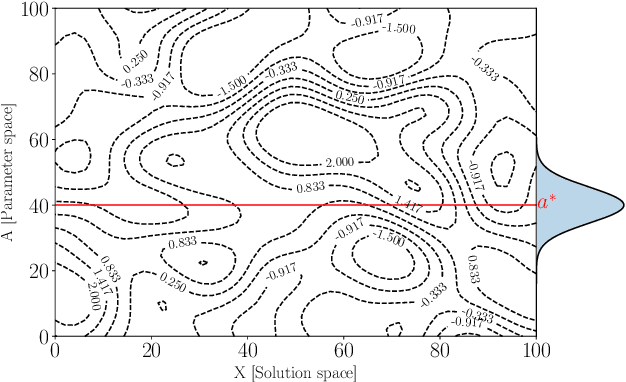
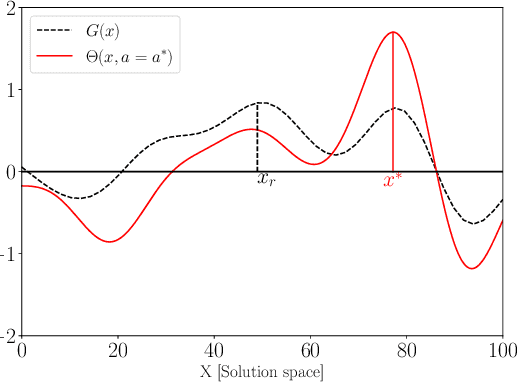
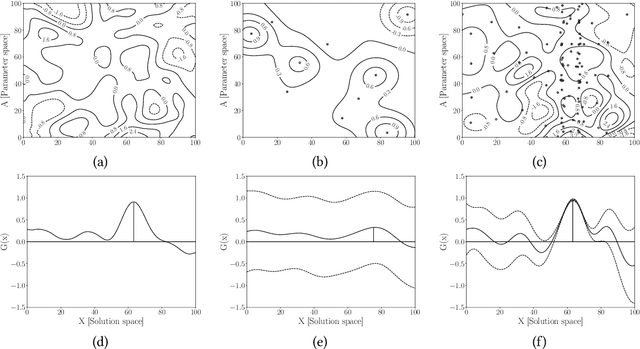
Simulators often require calibration inputs estimated from real world data and the quality of the estimate can significantly affect simulation output. Particularly when performing simulation optimisation to find an optimal solution, the uncertainty in the inputs significantly affects the quality of the found solution. One remedy is to search for the solution that has the best performance on average over the uncertain range of inputs yielding an optimal compromise solution. We consider the more general setting where a user may choose between either running simulations or instead collecting real world data. A user may choose an input and a solution and observe the simulation output, or instead query an external data source improving the input estimate enabling the search for a more focused, less compromised solution. We explicitly examine the trade-off between simulation and real data collection in order to find the optimal solution of the simulator with the true inputs. Using a value of information procedure, we propose a novel unified simulation optimisation procedure called Bayesian Information Collection and Optimisation (BICO) that, in each iteration, automatically determines which of the two actions (running simulations or data collection) is more beneficial. Numerical experiments demonstrate that the proposed algorithm is able to automatically determine an appropriate balance between optimisation and data collection.

ConBO: Conditional Bayesian Optimization

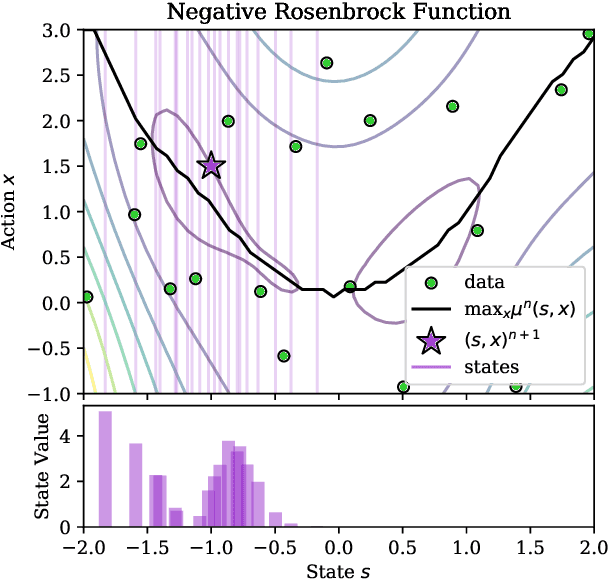
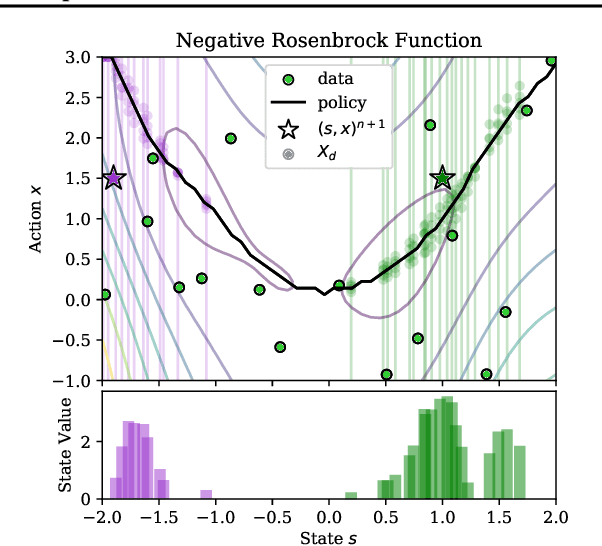
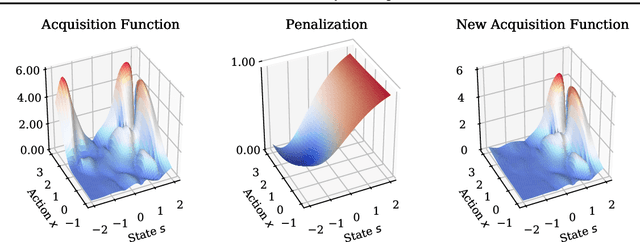
Bayesian optimization is a class of data efficient model based algorithms typically focused on global optimization. We consider the more general case where a user is faced with multiple problems that each need to be optimized conditional on a state variable, for example we optimize the location of ambulances conditioned on patient distribution given a range of cities with different patient distributions. Similarity across objectives boosts optimization of each objective in two ways: in modelling by data sharing across objectives, and also in acquisition by quantifying how all objectives benefit from a single point on one objective. For this we propose ConBO, a novel efficient algorithm that is based on a new hybrid Knowledge Gradient method, that outperforms recently published works on synthetic and real world problems, and is easily parallelized to collecting a batch of points.

Scalable Global Optimization via Local Bayesian Optimization

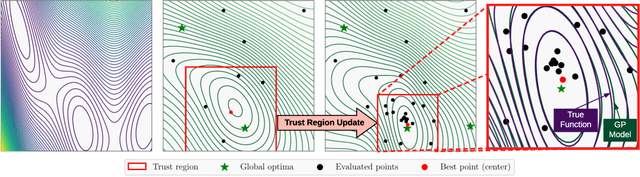
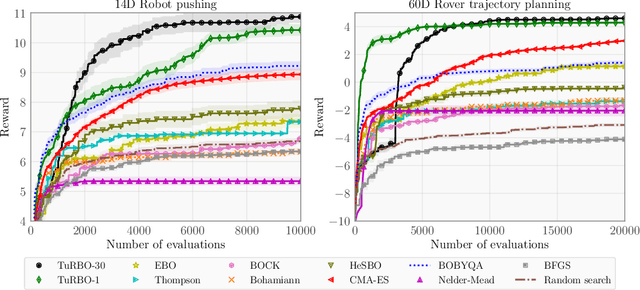
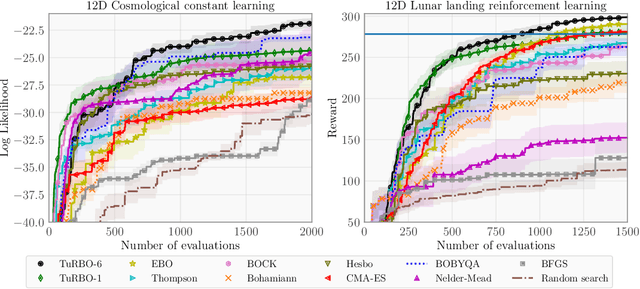
Bayesian optimization has recently emerged as a popular method for the sample-efficient optimization of expensive black-box functions. However, the application to high-dimensional problems with several thousand observations remains challenging, and on difficult problems Bayesian optimization is often not competitive with other paradigms. In this paper we take the view that this is due to the implicit homogeneity of the global probabilistic models and an overemphasized exploration that results from global acquisition. This motivates the design of a local probabilistic approach for global optimization of large-scale high-dimensional problems. We propose the $\texttt{TuRBO}$ algorithm that fits a collection of local models and performs a principled global allocation of samples across these models via an implicit bandit approach. A comprehensive evaluation demonstrates that $\texttt{TuRBO}$ outperforms state-of-the-art methods from machine learning and operations research on problems spanning reinforcement learning, robotics, and the natural sciences.

Bayesian Optimization Allowing for Common Random Numbers

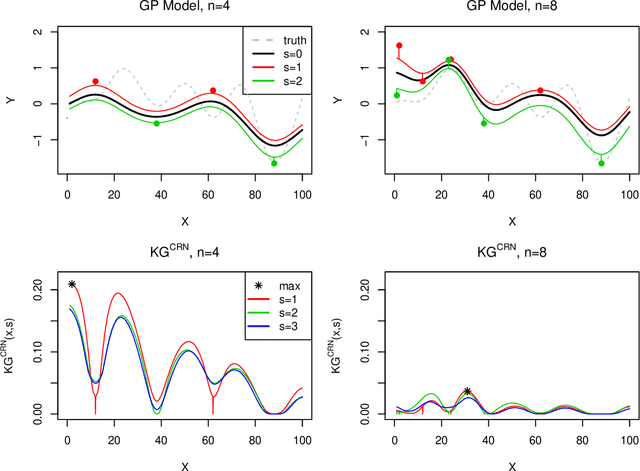
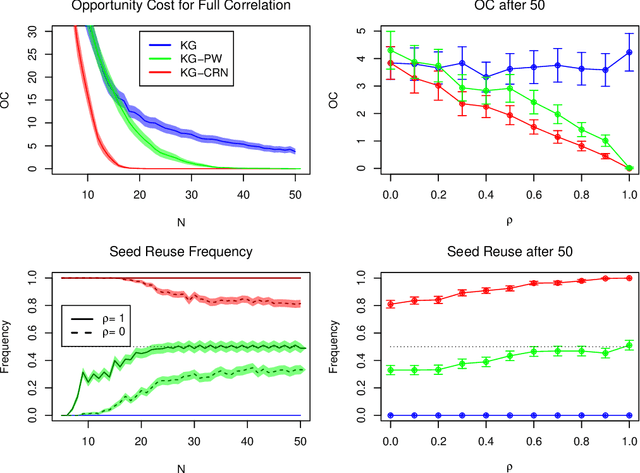
Bayesian optimization is a powerful tool for expensive stochastic black-box optimization problems such as simulation-based optimization or machine learning hyperparameter tuning. Many stochastic objective functions implicitly require a random number seed as input. By explicitly reusing a seed a user can exploit common random numbers, comparing two or more inputs under the same randomly generated scenario, such as a common customer stream in a job shop problem, or the same random partition of training data into training and validation set for a machine learning algorithm. With the aim of finding an input with the best average performance over infinitely many seeds, we propose a novel Gaussian process model that jointly models both the output for each seed and the average. We then introduce the Knowledge gradient for Common Random Numbers that iteratively determines a combination of input and random seed to evaluate the objective and automatically trades off reusing old seeds and querying new seeds, thus overcoming the need to evaluate inputs in batches or measuring differences of pairs as suggested in previous methods. We investigate the Knowledge Gradient for Common Random Numbers both theoretically and empirically, finding it achieves significant performance improvements with only moderate added computational cost.