Exploiting Transitivity for Top-k Selection with Score-Based Dueling Bandits

We consider the problem of top-k subset selection in Dueling Bandit problems with score information. Real-world pairwise ranking problems often exhibit a high degree of transitivity and prior work has suggested sampling methods that exploit such transitivity through the use of parametric preference models like the Bradley-Terry-Luce (BTL) and Thurstone models. To date, this work has focused on cases where sample outcomes are win/loss binary responses. We extend this to selection problems where sampling results contain quantitative information by proposing a Thurstonian style model and adapting the Pairwise Optimal Computing Budget Allocation for subset selection (POCBAm) sampling method to exploit this model for efficient sample selection. We compare the empirical performance against standard POCBAm and other competing algorithms.

ConBO: Conditional Bayesian Optimization

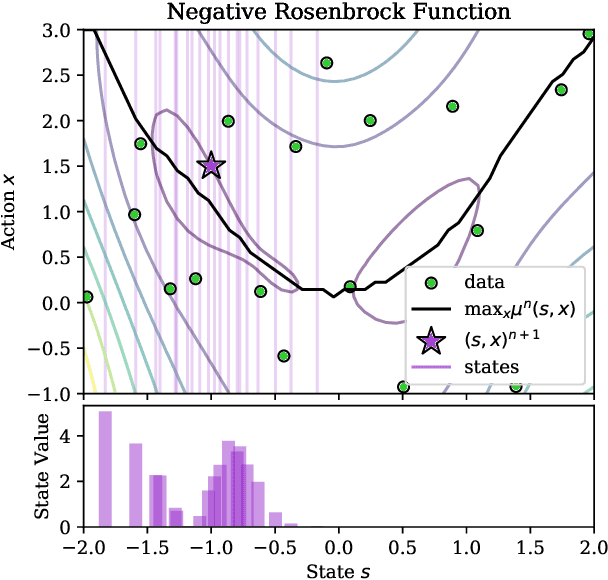
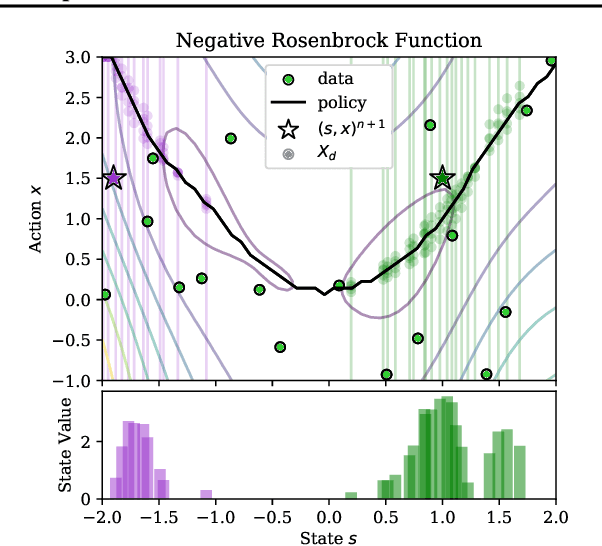
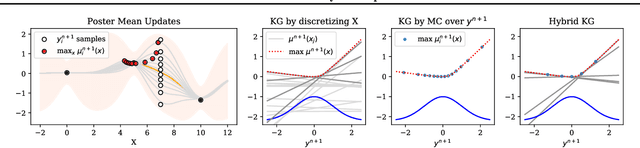
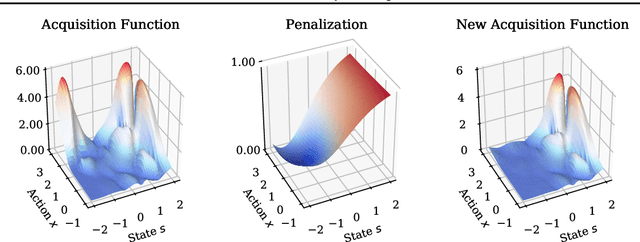
Bayesian optimization is a class of data efficient model based algorithms typically focused on global optimization. We consider the more general case where a user is faced with multiple problems that each need to be optimized conditional on a state variable, for example we optimize the location of ambulances conditioned on patient distribution given a range of cities with different patient distributions. Similarity across objectives boosts optimization of each objective in two ways: in modelling by data sharing across objectives, and also in acquisition by quantifying how all objectives benefit from a single point on one objective. For this we propose ConBO, a novel efficient algorithm that is based on a new hybrid Knowledge Gradient method, that outperforms recently published works on synthetic and real world problems, and is easily parallelized to collecting a batch of points.

Efficient and Scalable Batch Bayesian Optimization Using K-Means

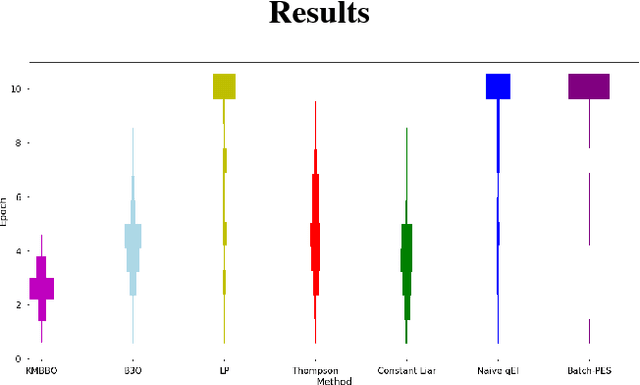
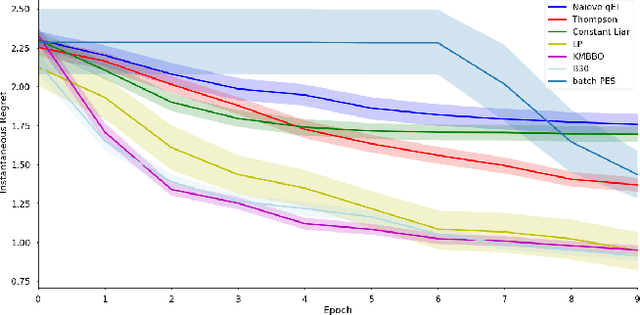
We present K-Means Batch Bayesian Optimization (KMBBO), a novel batch sampling algorithm for Bayesian Optimization (BO). KMBBO uses unsupervised learning to efficiently estimate peaks of the model acquisition function. We show in empirical experiments that our method outperforms the current state-of-the-art batch allocation algorithms on a variety of test problems including tuning of algorithm hyper-parameters and a challenging drug discovery problem. In order to accommodate the real-world problem of high dimensional data, we propose a modification to KMBBO by combining it with compressed sensing to project the optimization into a lower dimensional subspace. We demonstrate empirically that this 2-step method outperforms algorithms where no dimensionality reduction has taken place.