Fearless Stochasticity in Expectation Propagation

Expectation propagation (EP) is a family of algorithms for performing approximate inference in probabilistic models. The updates of EP involve the evaluation of moments -- expectations of certain functions -- which can be estimated from Monte Carlo (MC) samples. However, the updates are not robust to MC noise when performed naively, and various prior works have attempted to address this issue in different ways. In this work, we provide a novel perspective on the moment-matching updates of EP; namely, that they perform natural-gradient-based optimisation of a variational objective. We use this insight to motivate two new EP variants, with updates that are particularly well-suited to MC estimation; they remain stable and are most sample-efficient when estimated with just a single sample. These new variants combine the benefits of their predecessors and address key weaknesses. In particular, they are easier to tune, offer an improved speed-accuracy trade-off, and do not rely on the use of debiasing estimators. We demonstrate their efficacy on a variety of probabilistic inference tasks.

Estimating the normal-inverse-Wishart distribution

The normal-inverse-Wishart (NIW) distribution is commonly used as a prior distribution for the mean and covariance parameters of a multivariate normal distribution. The family of NIW distributions is also a minimal exponential family. In this short note we describe a convergent procedure for converting from mean parameters to natural parameters in the NIW family, or -- equivalently -- for performing maximum likelihood estimation of the natural parameters given observed sufficient statistics. This is needed, for example, when using a NIW base family in expectation propagation

Identifiable Feature Learning for Spatial Data with Nonlinear ICA

Recently, nonlinear ICA has surfaced as a popular alternative to the many heuristic models used in deep representation learning and disentanglement. An advantage of nonlinear ICA is that a sophisticated identifiability theory has been developed; in particular, it has been proven that the original components can be recovered under sufficiently strong latent dependencies. Despite this general theory, practical nonlinear ICA algorithms have so far been mainly limited to data with one-dimensional latent dependencies, especially time-series data. In this paper, we introduce a new nonlinear ICA framework that employs $t$-process (TP) latent components which apply naturally to data with higher-dimensional dependency structures, such as spatial and spatio-temporal data. In particular, we develop a new learning and inference algorithm that extends variational inference methods to handle the combination of a deep neural network mixing function with the TP prior, and employs the method of inducing points for computational efficacy. On the theoretical side, we show that such TP independent components are identifiable under very general conditions. Further, Gaussian Process (GP) nonlinear ICA is established as a limit of the TP Nonlinear ICA model, and we prove that the identifiability of the latent components at this GP limit is more restricted. Namely, those components are identifiable if and only if they have distinctly different covariance kernels. Our algorithm and identifiability theorems are explored on simulated spatial data and real world spatio-temporal data.

Optimising Distributions with Natural Gradient Surrogates

Natural gradient methods have been used to optimise the parameters of probability distributions in a variety of settings, often resulting in fast-converging procedures. Unfortunately, for many distributions of interest, computing the natural gradient has a number of challenges. In this work we propose a novel technique for tackling such issues, which involves reframing the optimisation as one with respect to the parameters of a surrogate distribution, for which computing the natural gradient is easy. We give several examples of existing methods that can be interpreted as applying this technique, and propose a new method for applying it to a wide variety of problems. Our method expands the set of distributions that can be efficiently targeted with natural gradients. Furthermore, it is fast, easy to understand, simple to implement using standard autodiff software, and does not require lengthy model-specific derivations. We demonstrate our method on maximum likelihood estimation and variational inference tasks.

Disentangling Identifiable Features from Noisy Data with Structured Nonlinear ICA

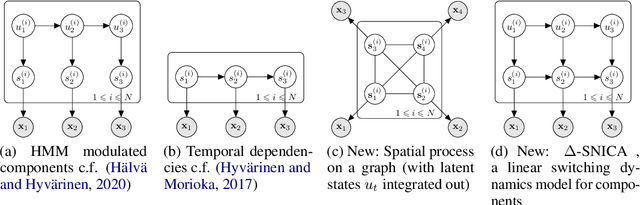
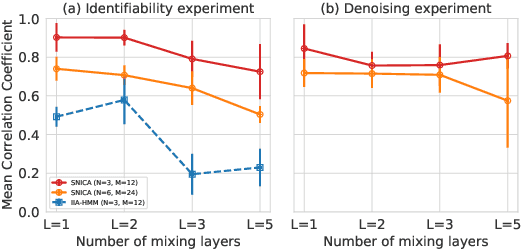
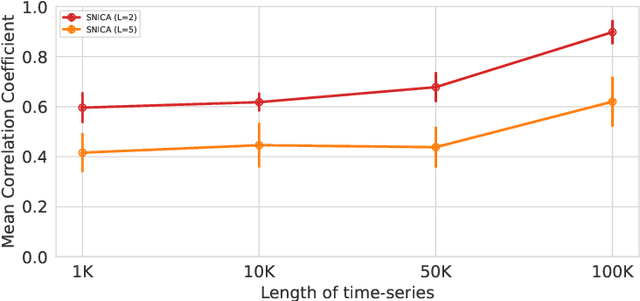
We introduce a new general identifiable framework for principled disentanglement referred to as Structured Nonlinear Independent Component Analysis (SNICA). Our contribution is to extend the identifiability theory of deep generative models for a very broad class of structured models. While previous works have shown identifiability for specific classes of time-series models, our theorems extend this to more general temporal structures as well as to models with more complex structures such as spatial dependencies. In particular, we establish the major result that identifiability for this framework holds even in the presence of noise of unknown distribution. The SNICA setting therefore subsumes all the existing nonlinear ICA models for time-series and also allows for new much richer identifiable models. Finally, as an example of our framework's flexibility, we introduce the first nonlinear ICA model for time-series that combines the following very useful properties: it accounts for both nonstationarity and autocorrelation in a fully unsupervised setting; performs dimensionality reduction; models hidden states; and enables principled estimation and inference by variational maximum-likelihood.

Sparse Gaussian Process Variational Autoencoders

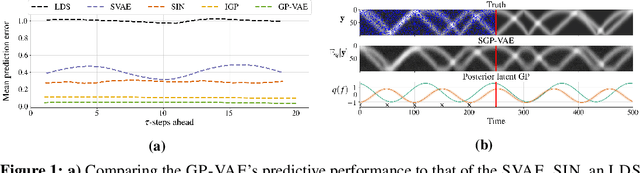
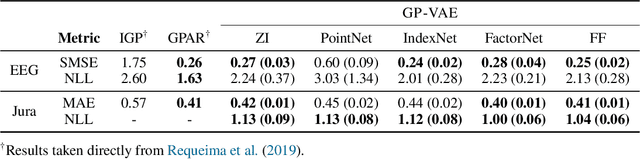
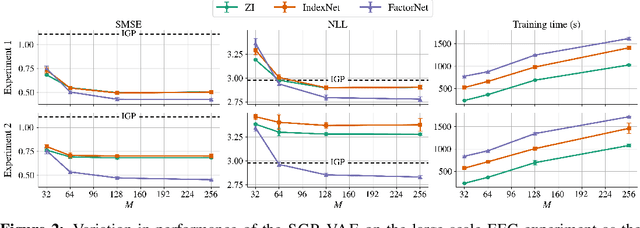
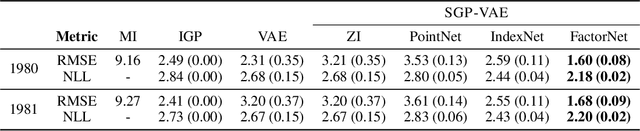
Large, multi-dimensional spatio-temporal datasets are omnipresent in modern science and engineering. An effective framework for handling such data are Gaussian process deep generative models (GP-DGMs), which employ GP priors over the latent variables of DGMs. Existing approaches for performing inference in GP-DGMs do not support sparse GP approximations based on inducing points, which are essential for the computational efficiency of GPs, nor do they handle missing data -- a natural occurrence in many spatio-temporal datasets -- in a principled manner. We address these shortcomings with the development of the sparse Gaussian process variational autoencoder (SGP-VAE), characterised by the use of partial inference networks for parameterising sparse GP approximations. Leveraging the benefits of amortised variational inference, the SGP-VAE enables inference in multi-output sparse GPs on previously unobserved data with no additional training. The SGP-VAE is evaluated in a variety of experiments where it outperforms alternative approaches including multi-output GPs and structured VAEs.