Identifiable Feature Learning for Spatial Data with Nonlinear ICA

Recently, nonlinear ICA has surfaced as a popular alternative to the many heuristic models used in deep representation learning and disentanglement. An advantage of nonlinear ICA is that a sophisticated identifiability theory has been developed; in particular, it has been proven that the original components can be recovered under sufficiently strong latent dependencies. Despite this general theory, practical nonlinear ICA algorithms have so far been mainly limited to data with one-dimensional latent dependencies, especially time-series data. In this paper, we introduce a new nonlinear ICA framework that employs $t$-process (TP) latent components which apply naturally to data with higher-dimensional dependency structures, such as spatial and spatio-temporal data. In particular, we develop a new learning and inference algorithm that extends variational inference methods to handle the combination of a deep neural network mixing function with the TP prior, and employs the method of inducing points for computational efficacy. On the theoretical side, we show that such TP independent components are identifiable under very general conditions. Further, Gaussian Process (GP) nonlinear ICA is established as a limit of the TP Nonlinear ICA model, and we prove that the identifiability of the latent components at this GP limit is more restricted. Namely, those components are identifiable if and only if they have distinctly different covariance kernels. Our algorithm and identifiability theorems are explored on simulated spatial data and real world spatio-temporal data.

Disentangling Identifiable Features from Noisy Data with Structured Nonlinear ICA

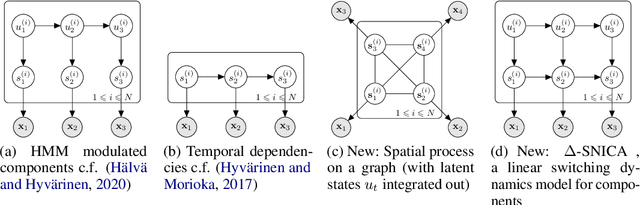
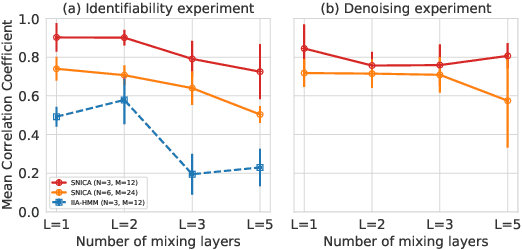
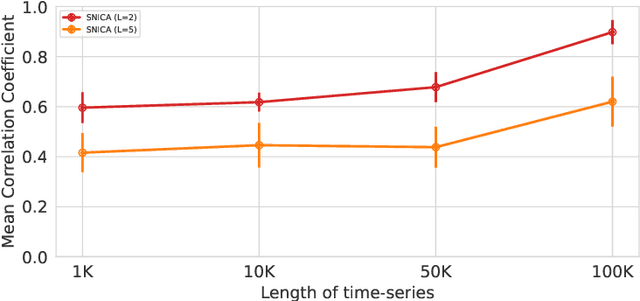
We introduce a new general identifiable framework for principled disentanglement referred to as Structured Nonlinear Independent Component Analysis (SNICA). Our contribution is to extend the identifiability theory of deep generative models for a very broad class of structured models. While previous works have shown identifiability for specific classes of time-series models, our theorems extend this to more general temporal structures as well as to models with more complex structures such as spatial dependencies. In particular, we establish the major result that identifiability for this framework holds even in the presence of noise of unknown distribution. The SNICA setting therefore subsumes all the existing nonlinear ICA models for time-series and also allows for new much richer identifiable models. Finally, as an example of our framework's flexibility, we introduce the first nonlinear ICA model for time-series that combines the following very useful properties: it accounts for both nonstationarity and autocorrelation in a fully unsupervised setting; performs dimensionality reduction; models hidden states; and enables principled estimation and inference by variational maximum-likelihood.

Hidden Markov Nonlinear ICA: Unsupervised Learning from Nonstationary Time Series

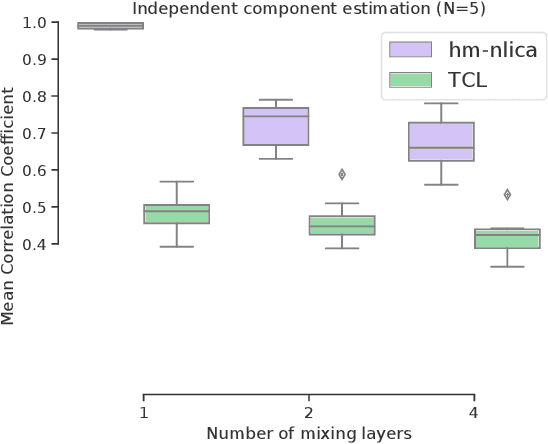
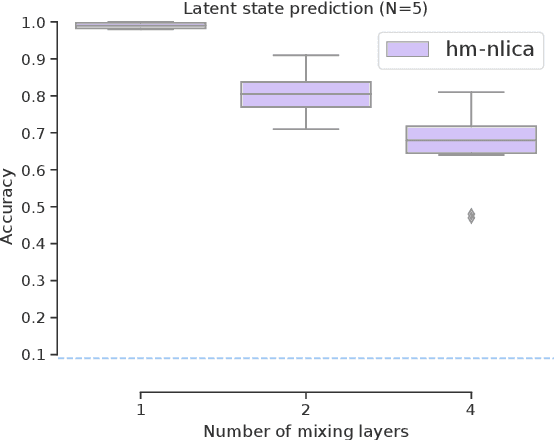
Recent advances in nonlinear Independent Component Analysis (ICA) provide a principled framework for unsupervised feature learning and disentanglement. The central idea in such works is that the latent components are assumed to be independent conditional on some observed auxiliary variables, such as the time-segment index. This requires manual segmentation of data into non-stationary segments which is computationally expensive, inaccurate and often impossible. These models are thus not fully unsupervised. We remedy these limitations by combining nonlinear ICA with a Hidden Markov Model, resulting in a model where a latent state acts in place of the observed segment-index. We prove identifiability of the proposed model for a general mixing nonlinearity, such as a neural network. We also show how maximum likelihood estimation of the model can be done using the expectation-maximization algorithm. Thus, we achieve a new nonlinear ICA framework which is unsupervised, more efficient, as well as able to model underlying temporal dynamics.

Computational Graph Approach for Detection of Composite Human Activities

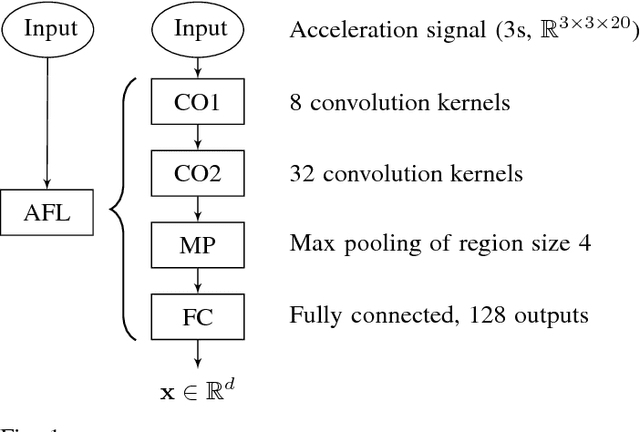
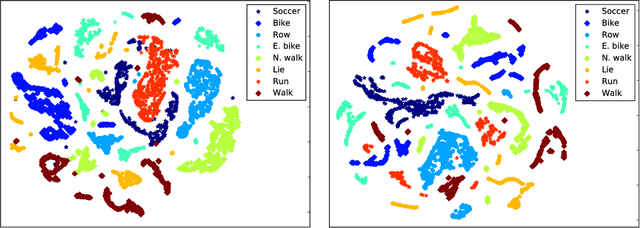
Existing work in human activity detection classifies physical activities using a single fixed-length subset of a sensor signal. However, temporally consecutive subsets of a sensor signal are not utilized. This is not optimal for classifying physical activities (composite activities) that are composed of a temporal series of simpler activities (atomic activities). A sport consists of physical activities combined in a fashion unique to that sport. The constituent physical activities and the sport are not fundamentally different. We propose a computational graph architecture for human activity detection based on the readings of a triaxial accelerometer. The resulting model learns 1) a representation of the atomic activities of a sport and 2) to classify physical activities as compositions of the atomic activities. The proposed model, alongside with a set of baseline models, was tested for a simultaneous classification of eight physical activities (walking, nordic walking, running, soccer, rowing, bicycling, exercise bicycling and lying down). The proposed model obtained an overall mean accuracy of 77.91% (population) and 95.28% (personalized). The corresponding accuracies of the best baseline model were 73.52% and 90.03%. However, without combining consecutive atomic activities, the corresponding accuracies of the proposed model were 71.52% and 91.22%. The results show that our proposed model is accurate, outperforms the baseline models and learns to combine simple activities into complex activities. Composite activities can be classified as combinations of atomic activities. Our proposed architecture is a basis for accurate models in human activity detection.