Bencher: Simple and Reproducible Benchmarking for Black-Box Optimization

We present Bencher, a modular benchmarking framework for black-box optimization that fundamentally decouples benchmark execution from optimization logic. Unlike prior suites that focus on combining many benchmarks in a single project, Bencher introduces a clean abstraction boundary: each benchmark is isolated in its own virtual Python environment and accessed via a unified, version-agnostic remote procedure call (RPC) interface. This design eliminates dependency conflicts and simplifies the integration of diverse, real-world benchmarks, which often have complex and conflicting software requirements. Bencher can be deployed locally or remotely via Docker or on high-performance computing (HPC) clusters via Singularity, providing a containerized, reproducible runtime for any benchmark. Its lightweight client requires minimal setup and supports drop-in evaluation of 80 benchmarks across continuous, categorical, and binary domains.

Leveraging Axis-Aligned Subspaces for High-Dimensional Bayesian Optimization with Group Testing

Bayesian optimization (BO ) is an effective method for optimizing expensive-to-evaluate black-box functions. While high-dimensional problems can be particularly challenging, due to the multitude of parameter choices and the potentially high number of data points required to fit the model, this limitation can be addressed if the problem satisfies simplifying assumptions. Axis-aligned subspace approaches, where few dimensions have a significant impact on the objective, motivated several algorithms for high-dimensional BO . However, the validity of this assumption is rarely verified, and the assumption is rarely exploited to its full extent. We propose a group testing ( GT) approach to identify active variables to facilitate efficient optimization in these domains. The proposed algorithm, Group Testing Bayesian Optimization (GTBO), first runs a testing phase where groups of variables are systematically selected and tested on whether they influence the objective, then terminates once active dimensions are identified. To that end, we extend the well-established GT theory to functions over continuous domains. In the second phase, GTBO guides optimization by placing more importance on the active dimensions. By leveraging the axis-aligned subspace assumption, GTBO outperforms state-of-the-art methods on benchmarks satisfying the assumption of axis-aligned subspaces, while offering improved interpretability.

Understanding High-Dimensional Bayesian Optimization

Recent work reported that simple Bayesian optimization methods perform well for high-dimensional real-world tasks, seemingly contradicting prior work and tribal knowledge. This paper investigates the 'why'. We identify fundamental challenges that arise in high-dimensional Bayesian optimization and explain why recent methods succeed. Our analysis shows that vanishing gradients caused by Gaussian process initialization schemes play a major role in the failures of high-dimensional Bayesian optimization and that methods that promote local search behaviors are better suited for the task. We find that maximum likelihood estimation of Gaussian process length scales suffices for state-of-the-art performance. Based on this, we propose a simple variant of maximum likelihood estimation called MSR that leverages these findings to achieve state-of-the-art performance on a comprehensive set of real-world applications. We also present targeted experiments to illustrate and confirm our findings.

Exploring Exploration in Bayesian Optimization

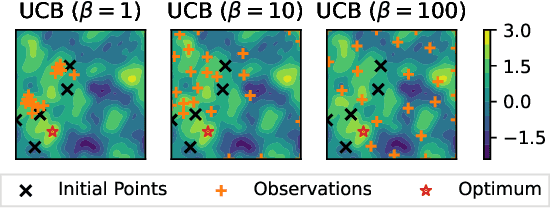
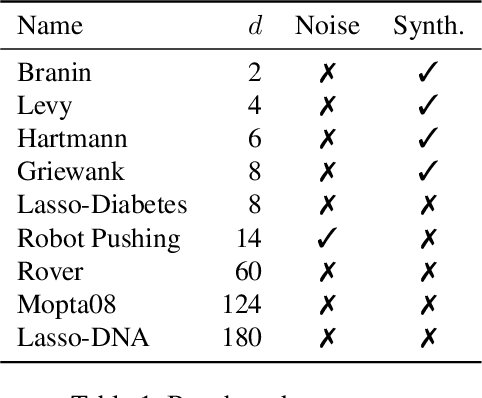
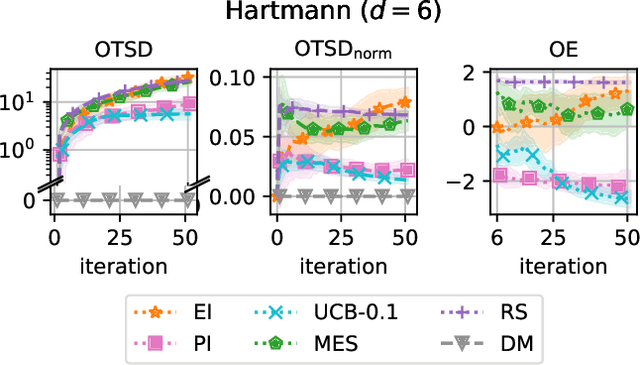
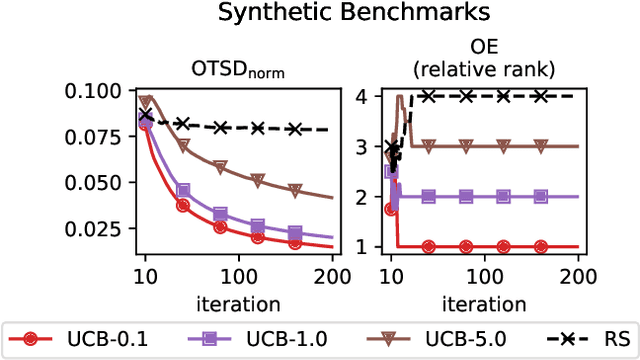
A well-balanced exploration-exploitation trade-off is crucial for successful acquisition functions in Bayesian optimization. However, there is a lack of quantitative measures for exploration, making it difficult to analyze and compare different acquisition functions. This work introduces two novel approaches - observation traveling salesman distance and observation entropy - to quantify the exploration characteristics of acquisition functions based on their selected observations. Using these measures, we examine the explorative nature of several well-known acquisition functions across a diverse set of black-box problems, uncover links between exploration and empirical performance, and reveal new relationships among existing acquisition functions. Beyond enabling a deeper understanding of acquisition functions, these measures also provide a foundation for guiding their design in a more principled and systematic manner.

A Unified Framework for Entropy Search and Expected Improvement in Bayesian Optimization

Bayesian optimization is a widely used method for optimizing expensive black-box functions, with Expected Improvement being one of the most commonly used acquisition functions. In contrast, information-theoretic acquisition functions aim to reduce uncertainty about the function's optimum and are often considered fundamentally distinct from EI. In this work, we challenge this prevailing perspective by introducing a unified theoretical framework, Variational Entropy Search, which reveals that EI and information-theoretic acquisition functions are more closely related than previously recognized. We demonstrate that EI can be interpreted as a variational inference approximation of the popular information-theoretic acquisition function, named Max-value Entropy Search. Building on this insight, we propose VES-Gamma, a novel acquisition function that balances the strengths of EI and MES. Extensive empirical evaluations across both low- and high-dimensional synthetic and real-world benchmarks demonstrate that VES-Gamma is competitive with state-of-the-art acquisition functions and in many cases outperforms EI and MES.

CATBench: A Compiler Autotuning Benchmarking Suite for Black-box Optimization

Bayesian optimization is a powerful method for automating tuning of compilers. The complex landscape of autotuning provides a myriad of rarely considered structural challenges for black-box optimizers, and the lack of standardized benchmarks has limited the study of Bayesian optimization within the domain. To address this, we present CATBench, a comprehensive benchmarking suite that captures the complexities of compiler autotuning, ranging from discrete, conditional, and permutation parameter types to known and unknown binary constraints, as well as both multi-fidelity and multi-objective evaluations. The benchmarks in CATBench span a range of machine learning-oriented computations, from tensor algebra to image processing and clustering, and uses state-of-the-art compilers, such as TACO and RISE/ELEVATE. CATBench offers a unified interface for evaluating Bayesian optimization algorithms, promoting reproducibility and innovation through an easy-to-use, fully containerized setup of both surrogate and real-world compiler optimization tasks. We validate CATBench on several state-of-the-art algorithms, revealing their strengths and weaknesses and demonstrating the suite's potential for advancing both Bayesian optimization and compiler autotuning research.

Vanilla Bayesian Optimization Performs Great in High Dimensions

High-dimensional problems have long been considered the Achilles' heel of Bayesian optimization algorithms. Spurred by the curse of dimensionality, a large collection of algorithms aim to make it more performant in this setting, commonly by imposing various simplifying assumptions on the objective. In this paper, we identify the degeneracies that make vanilla Bayesian optimization poorly suited to high-dimensional tasks, and further show how existing algorithms address these degeneracies through the lens of lowering the model complexity. Moreover, we propose an enhancement to the prior assumptions that are typical to vanilla Bayesian optimization algorithms, which reduces the complexity to manageable levels without imposing structural restrictions on the objective. Our modification - a simple scaling of the Gaussian process lengthscale prior with the dimensionality - reveals that standard Bayesian optimization works drastically better than previously thought in high dimensions, clearly outperforming existing state-of-the-art algorithms on multiple commonly considered real-world high-dimensional tasks.

A General Framework for User-Guided Bayesian Optimization

The optimization of expensive-to-evaluate black-box functions is prevalent in various scientific disciplines. Bayesian optimization is an automatic, general and sample-efficient method to solve these problems with minimal knowledge of the underlying function dynamics. However, the ability of Bayesian optimization to incorporate prior knowledge or beliefs about the function at hand in order to accelerate the optimization is limited, which reduces its appeal for knowledgeable practitioners with tight budgets. To allow domain experts to customize the optimization routine, we propose ColaBO, the first Bayesian-principled framework for incorporating prior beliefs beyond the typical kernel structure, such as the likely location of the optimizer or the optimal value. The generality of ColaBO makes it applicable across different Monte Carlo acquisition functions and types of user beliefs. We empirically demonstrate ColaBO's ability to substantially accelerate optimization when the prior information is accurate, and to retain approximately default performance when it is misleading.

High-dimensional Bayesian Optimization with Group Testing

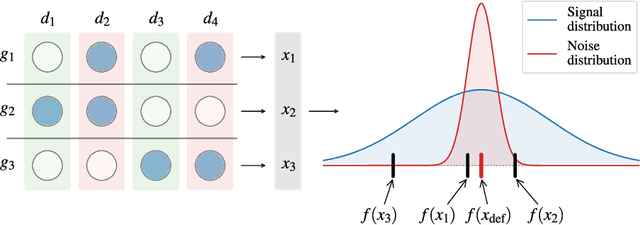
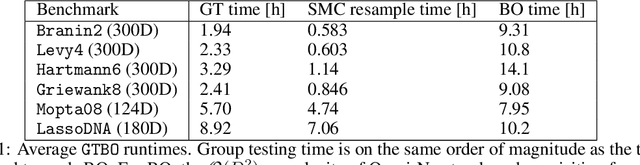
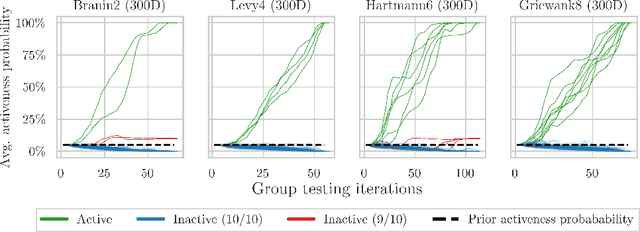
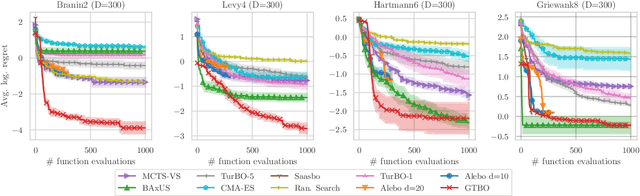
Bayesian optimization is an effective method for optimizing expensive-to-evaluate black-box functions. High-dimensional problems are particularly challenging as the surrogate model of the objective suffers from the curse of dimensionality, which makes accurate modeling difficult. We propose a group testing approach to identify active variables to facilitate efficient optimization in these domains. The proposed algorithm, Group Testing Bayesian Optimization (GTBO), first runs a testing phase where groups of variables are systematically selected and tested on whether they influence the objective. To that end, we extend the well-established theory of group testing to functions of continuous ranges. In the second phase, GTBO guides optimization by placing more importance on the active dimensions. By exploiting the axis-aligned subspace assumption, GTBO is competitive against state-of-the-art methods on several synthetic and real-world high-dimensional optimization tasks. Furthermore, GTBO aids in the discovery of active parameters in applications, thereby enhancing practitioners' understanding of the problem at hand.

Bounce: a Reliable Bayesian Optimization Algorithm for Combinatorial and Mixed Spaces

Impactful applications such as materials discovery, hardware design, neural architecture search, or portfolio optimization require optimizing high-dimensional black-box functions with mixed and combinatorial input spaces. While Bayesian optimization has recently made significant progress in solving such problems, an in-depth analysis reveals that the current state-of-the-art methods are not reliable. Their performances degrade substantially when the unknown optima of the function do not have a certain structure. To fill the need for a reliable algorithm for combinatorial and mixed spaces, this paper proposes Bounce that relies on a novel map of various variable types into nested embeddings of increasing dimensionality. Comprehensive experiments show that Bounce reliably achieves and often even improves upon state-of-the-art performance on a variety of high-dimensional problems.