CATBench: A Compiler Autotuning Benchmarking Suite for Black-box Optimization

Bayesian optimization is a powerful method for automating tuning of compilers. The complex landscape of autotuning provides a myriad of rarely considered structural challenges for black-box optimizers, and the lack of standardized benchmarks has limited the study of Bayesian optimization within the domain. To address this, we present CATBench, a comprehensive benchmarking suite that captures the complexities of compiler autotuning, ranging from discrete, conditional, and permutation parameter types to known and unknown binary constraints, as well as both multi-fidelity and multi-objective evaluations. The benchmarks in CATBench span a range of machine learning-oriented computations, from tensor algebra to image processing and clustering, and uses state-of-the-art compilers, such as TACO and RISE/ELEVATE. CATBench offers a unified interface for evaluating Bayesian optimization algorithms, promoting reproducibility and innovation through an easy-to-use, fully containerized setup of both surrogate and real-world compiler optimization tasks. We validate CATBench on several state-of-the-art algorithms, revealing their strengths and weaknesses and demonstrating the suite's potential for advancing both Bayesian optimization and compiler autotuning research.

Vanilla Bayesian Optimization Performs Great in High Dimensions

High-dimensional problems have long been considered the Achilles' heel of Bayesian optimization algorithms. Spurred by the curse of dimensionality, a large collection of algorithms aim to make it more performant in this setting, commonly by imposing various simplifying assumptions on the objective. In this paper, we identify the degeneracies that make vanilla Bayesian optimization poorly suited to high-dimensional tasks, and further show how existing algorithms address these degeneracies through the lens of lowering the model complexity. Moreover, we propose an enhancement to the prior assumptions that are typical to vanilla Bayesian optimization algorithms, which reduces the complexity to manageable levels without imposing structural restrictions on the objective. Our modification - a simple scaling of the Gaussian process lengthscale prior with the dimensionality - reveals that standard Bayesian optimization works drastically better than previously thought in high dimensions, clearly outperforming existing state-of-the-art algorithms on multiple commonly considered real-world high-dimensional tasks.

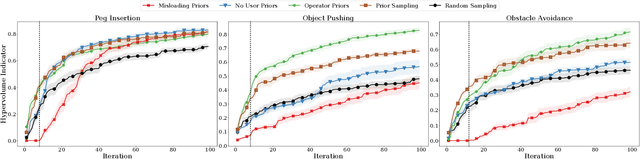
A General Framework for User-Guided Bayesian Optimization

The optimization of expensive-to-evaluate black-box functions is prevalent in various scientific disciplines. Bayesian optimization is an automatic, general and sample-efficient method to solve these problems with minimal knowledge of the underlying function dynamics. However, the ability of Bayesian optimization to incorporate prior knowledge or beliefs about the function at hand in order to accelerate the optimization is limited, which reduces its appeal for knowledgeable practitioners with tight budgets. To allow domain experts to customize the optimization routine, we propose ColaBO, the first Bayesian-principled framework for incorporating prior beliefs beyond the typical kernel structure, such as the likely location of the optimizer or the optimal value. The generality of ColaBO makes it applicable across different Monte Carlo acquisition functions and types of user beliefs. We empirically demonstrate ColaBO's ability to substantially accelerate optimization when the prior information is accurate, and to retain approximately default performance when it is misleading.

High-dimensional Bayesian Optimization with Group Testing

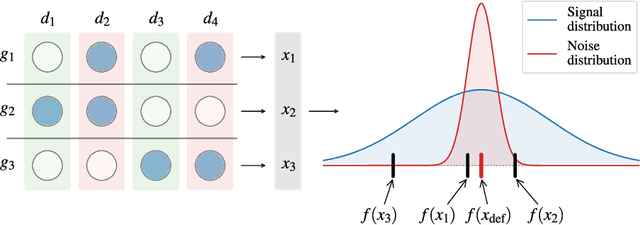
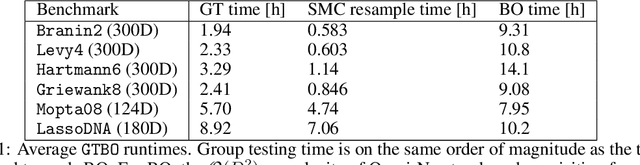
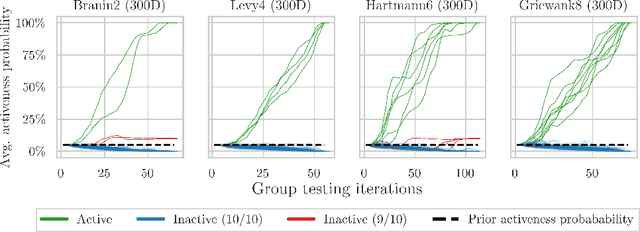
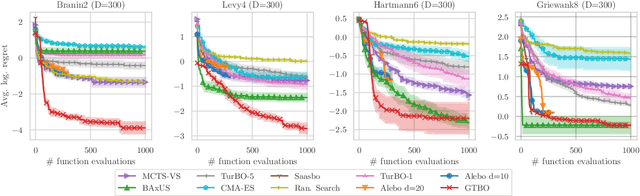
Bayesian optimization is an effective method for optimizing expensive-to-evaluate black-box functions. High-dimensional problems are particularly challenging as the surrogate model of the objective suffers from the curse of dimensionality, which makes accurate modeling difficult. We propose a group testing approach to identify active variables to facilitate efficient optimization in these domains. The proposed algorithm, Group Testing Bayesian Optimization (GTBO), first runs a testing phase where groups of variables are systematically selected and tested on whether they influence the objective. To that end, we extend the well-established theory of group testing to functions of continuous ranges. In the second phase, GTBO guides optimization by placing more importance on the active dimensions. By exploiting the axis-aligned subspace assumption, GTBO is competitive against state-of-the-art methods on several synthetic and real-world high-dimensional optimization tasks. Furthermore, GTBO aids in the discovery of active parameters in applications, thereby enhancing practitioners' understanding of the problem at hand.

PriorBand: Practical Hyperparameter Optimization in the Age of Deep Learning

Hyperparameters of Deep Learning (DL) pipelines are crucial for their downstream performance. While a large number of methods for Hyperparameter Optimization (HPO) have been developed, their incurred costs are often untenable for modern DL. Consequently, manual experimentation is still the most prevalent approach to optimize hyperparameters, relying on the researcher's intuition, domain knowledge, and cheap preliminary explorations. To resolve this misalignment between HPO algorithms and DL researchers, we propose PriorBand, an HPO algorithm tailored to DL, able to utilize both expert beliefs and cheap proxy tasks. Empirically, we demonstrate PriorBand's efficiency across a range of DL benchmarks and show its gains under informative expert input and robustness against poor expert beliefs

Self-Correcting Bayesian Optimization through Bayesian Active Learning

Gaussian processes are cemented as the model of choice in Bayesian optimization and active learning. Yet, they are severely dependent on cleverly chosen hyperparameters to reach their full potential, and little effort is devoted to finding the right hyperparameters in the literature. We demonstrate the impact of selecting good hyperparameters for GPs and present two acquisition functions that explicitly prioritize this goal. Statistical distance-based Active Learning (SAL) considers the average disagreement among samples from the posterior, as measured by a statistical distance. It is shown to outperform the state-of-the-art in Bayesian active learning on a number of test functions. We then introduce Self-Correcting Bayesian Optimization (SCoreBO), which extends SAL to perform Bayesian optimization and active hyperparameter learning simultaneously. SCoreBO learns the model hyperparameters at improved rates compared to vanilla BO, while outperforming the latest Bayesian optimization methods on traditional benchmarks. Moreover, the importance of self-correction is demonstrated on an array of exotic Bayesian optimization tasks

Learning Skill-based Industrial Robot Tasks with User Priors

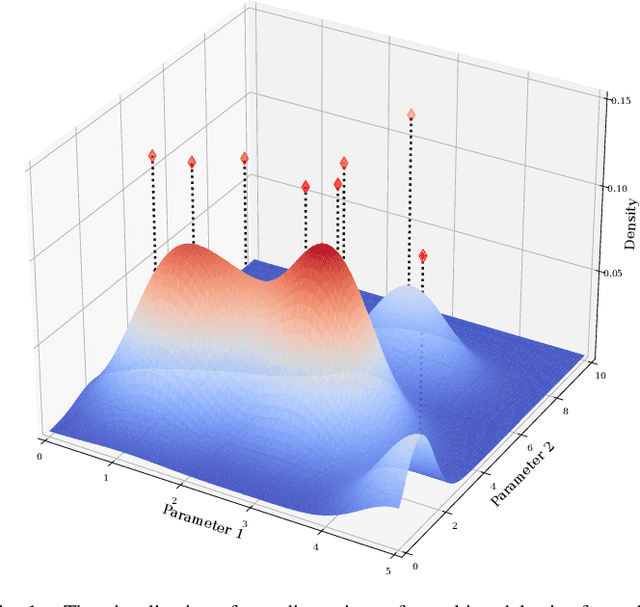
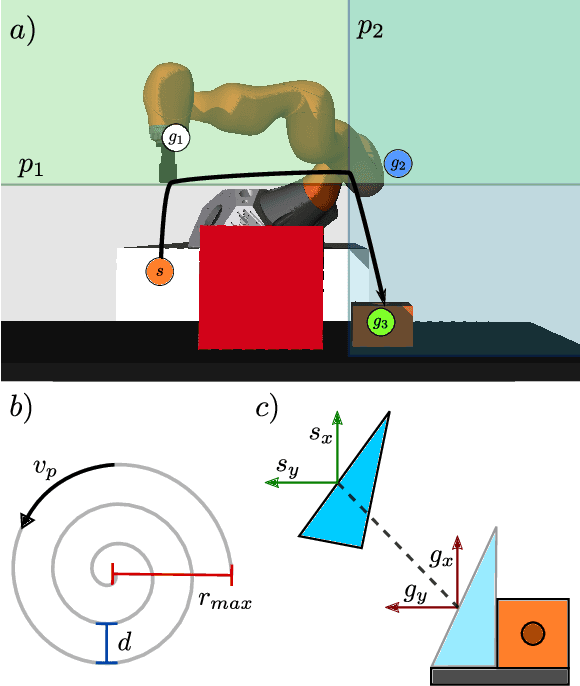
Robot skills systems are meant to reduce robot setup time for new manufacturing tasks. Yet, for dexterous, contact-rich tasks, it is often difficult to find the right skill parameters. One strategy is to learn these parameters by allowing the robot system to learn directly on the task. For a learning problem, a robot operator can typically specify the type and range of values of the parameters. Nevertheless, given their prior experience, robot operators should be able to help the learning process further by providing educated guesses about where in the parameter space potential optimal solutions could be found. Interestingly, such prior knowledge is not exploited in current robot learning frameworks. We introduce an approach that combines user priors and Bayesian optimization to allow fast optimization of robot industrial tasks at robot deployment time. We evaluate our method on three tasks that are learned in simulation as well as on two tasks that are learned directly on a real robot system. Additionally, we transfer knowledge from the corresponding simulation tasks by automatically constructing priors from well-performing configurations for learning on the real system. To handle potentially contradicting task objectives, the tasks are modeled as multi-objective problems. Our results show that operator priors, both user-specified and transferred, vastly accelerate the discovery of rich Pareto fronts, and typically produce final performance far superior to proposed baselines.

Joint Entropy Search For Maximally-Informed Bayesian Optimization

Information-theoretic Bayesian optimization techniques have become popular for optimizing expensive-to-evaluate black-box functions due to their non-myopic qualities. Entropy Search and Predictive Entropy Search both consider the entropy over the optimum in the input space, while the recent Max-value Entropy Search considers the entropy over the optimal value in the output space. We propose Joint Entropy Search (JES), a novel information-theoretic acquisition function that considers an entirely new quantity, namely the entropy over the joint optimal probability density over both input and output space. To incorporate this information, we consider the reduction in entropy from conditioning on fantasized optimal input/output pairs. The resulting approach primarily relies on standard GP machinery and removes complex approximations typically associated with information-theoretic methods. With minimal computational overhead, JES shows superior decision-making, and yields state-of-the-art performance for information-theoretic approaches across a wide suite of tasks. As a light-weight approach with superior results, JES provides a new go-to acquisition function for Bayesian optimization.

$π$BO: Augmenting Acquisition Functions with User Beliefs for Bayesian Optimization

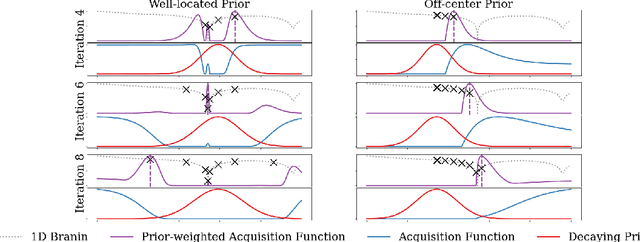
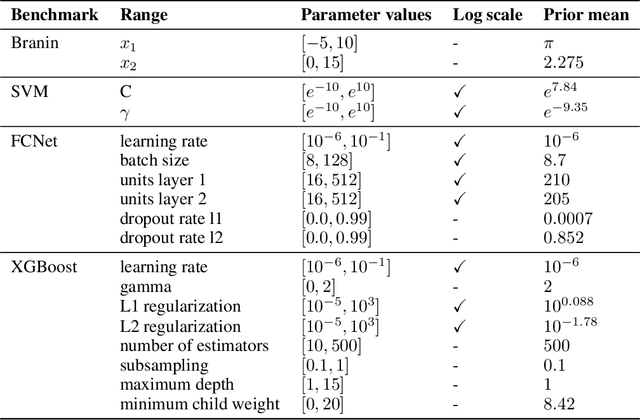
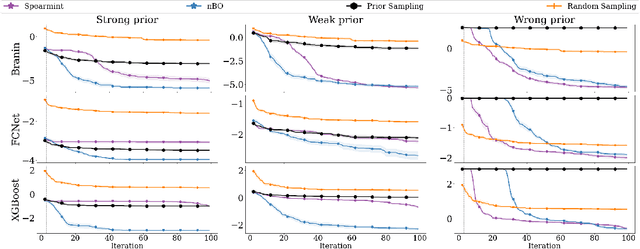
Bayesian optimization (BO) has become an established framework and popular tool for hyperparameter optimization (HPO) of machine learning (ML) algorithms. While known for its sample-efficiency, vanilla BO can not utilize readily available prior beliefs the practitioner has on the potential location of the optimum. Thus, BO disregards a valuable source of information, reducing its appeal to ML practitioners. To address this issue, we propose $\pi$BO, an acquisition function generalization which incorporates prior beliefs about the location of the optimum in the form of a probability distribution, provided by the user. In contrast to previous approaches, $\pi$BO is conceptually simple and can easily be integrated with existing libraries and many acquisition functions. We provide regret bounds when $\pi$BO is applied to the common Expected Improvement acquisition function and prove convergence at regular rates independently of the prior. Further, our experiments show that $\pi$BO outperforms competing approaches across a wide suite of benchmarks and prior characteristics. We also demonstrate that $\pi$BO improves on the state-of-the-art performance for a popular deep learning task, with a 12.5 $\times$ time-to-accuracy speedup over prominent BO approaches.