Ethan Caballero
Broken Neural Scaling Laws
Nov 10, 2022Abstract:We present a smoothly broken power law functional form that accurately models and extrapolates the scaling behaviors of deep neural networks (i.e. how the evaluation metric of interest varies as the amount of compute used for training, number of model parameters, training dataset size, or upstream performance varies) for each task within a large and diverse set of upstream and downstream tasks, in zero-shot, prompted, and fine-tuned settings. This set includes large-scale vision and unsupervised language tasks, diffusion generative modeling of images, arithmetic, and reinforcement learning. When compared to other functional forms for neural scaling behavior, this functional form yields extrapolations of scaling behavior that are considerably more accurate on this set. Moreover, this functional form accurately models and extrapolates scaling behavior that other functional forms are incapable of expressing such as the non-monotonic transitions present in the scaling behavior of phenomena such as double descent and the delayed, sharp inflection points present in the scaling behavior of tasks such as arithmetic. Lastly, we use this functional form to glean insights about the limit of the predictability of scaling behavior. Code is available at https://github.com/ethancaballero/broken_neural_scaling_laws
Scaling Laws for the Few-Shot Adaptation of Pre-trained Image Classifiers
Oct 18, 2021



Abstract:Empirical science of neural scaling laws is a rapidly growing area of significant importance to the future of machine learning, particularly in the light of recent breakthroughs achieved by large-scale pre-trained models such as GPT-3, CLIP and DALL-e. Accurately predicting the neural network performance with increasing resources such as data, compute and model size provides a more comprehensive evaluation of different approaches across multiple scales, as opposed to traditional point-wise comparisons of fixed-size models on fixed-size benchmarks, and, most importantly, allows for focus on the best-scaling, and thus most promising in the future, approaches. In this work, we consider a challenging problem of few-shot learning in image classification, especially when the target data distribution in the few-shot phase is different from the source, training, data distribution, in a sense that it includes new image classes not encountered during training. Our current main goal is to investigate how the amount of pre-training data affects the few-shot generalization performance of standard image classifiers. Our key observations are that (1) such performance improvements are well-approximated by power laws (linear log-log plots) as the training set size increases, (2) this applies to both cases of target data coming from either the same or from a different domain (i.e., new classes) as the training data, and (3) few-shot performance on new classes converges at a faster rate than the standard classification performance on previously seen classes. Our findings shed new light on the relationship between scale and generalization.
Invariance Principle Meets Information Bottleneck for Out-of-Distribution Generalization
Jun 11, 2021



Abstract:The invariance principle from causality is at the heart of notable approaches such as invariant risk minimization (IRM) that seek to address out-of-distribution (OOD) generalization failures. Despite the promising theory, invariance principle-based approaches fail in common classification tasks, where invariant (causal) features capture all the information about the label. Are these failures due to the methods failing to capture the invariance? Or is the invariance principle itself insufficient? To answer these questions, we revisit the fundamental assumptions in linear regression tasks, where invariance-based approaches were shown to provably generalize OOD. In contrast to the linear regression tasks, we show that for linear classification tasks we need much stronger restrictions on the distribution shifts, or otherwise OOD generalization is impossible. Furthermore, even with appropriate restrictions on distribution shifts in place, we show that the invariance principle alone is insufficient. We prove that a form of the information bottleneck constraint along with invariance helps address key failures when invariant features capture all the information about the label and also retains the existing success when they do not. We propose an approach that incorporates both of these principles and demonstrate its effectiveness in several experiments.
In Search of Robust Measures of Generalization
Oct 22, 2020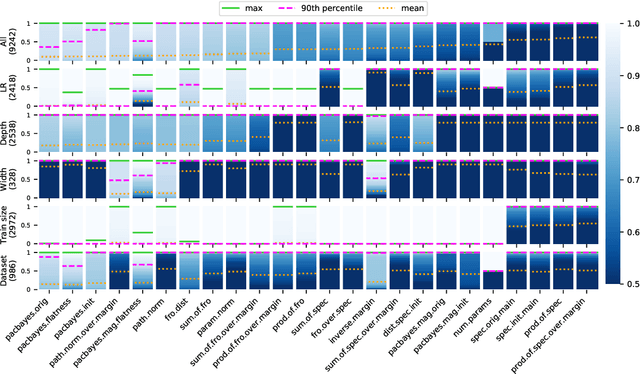
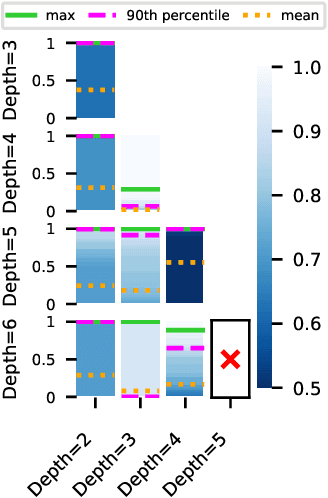
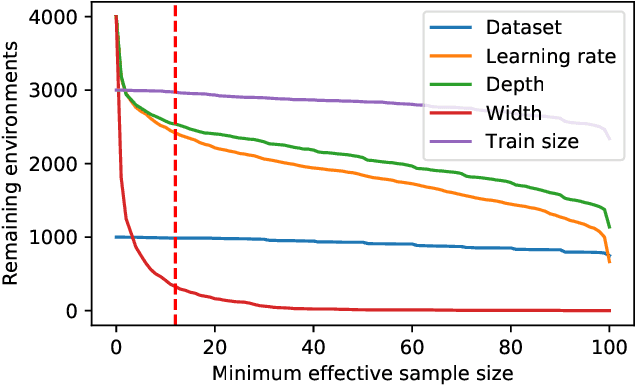
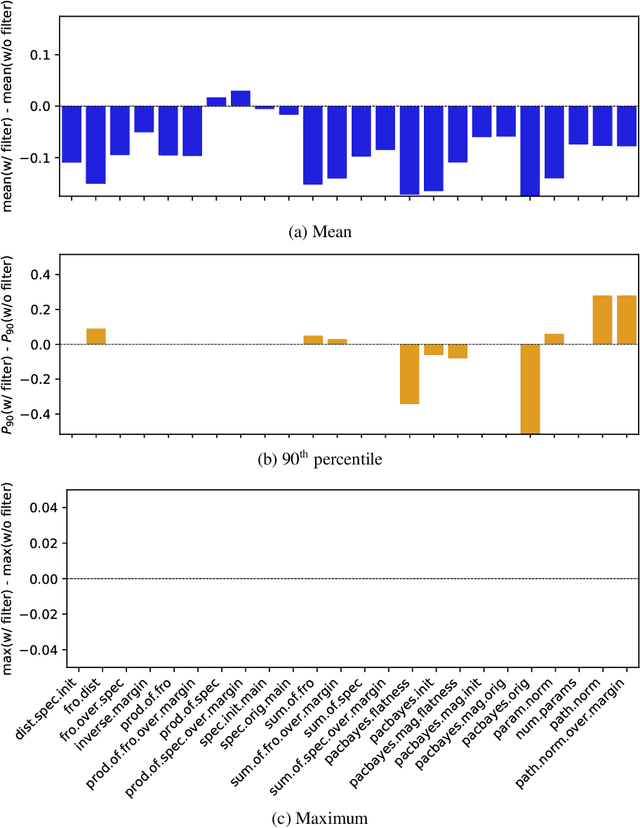
Abstract:One of the principal scientific challenges in deep learning is explaining generalization, i.e., why the particular way the community now trains networks to achieve small training error also leads to small error on held-out data from the same population. It is widely appreciated that some worst-case theories -- such as those based on the VC dimension of the class of predictors induced by modern neural network architectures -- are unable to explain empirical performance. A large volume of work aims to close this gap, primarily by developing bounds on generalization error, optimization error, and excess risk. When evaluated empirically, however, most of these bounds are numerically vacuous. Focusing on generalization bounds, this work addresses the question of how to evaluate such bounds empirically. Jiang et al. (2020) recently described a large-scale empirical study aimed at uncovering potential causal relationships between bounds/measures and generalization. Building on their study, we highlight where their proposed methods can obscure failures and successes of generalization measures in explaining generalization. We argue that generalization measures should instead be evaluated within the framework of distributional robustness.
Out-of-Distribution Generalization via Risk Extrapolation (REx)
Mar 13, 2020



Abstract:Generalizing outside of the training distribution is an open challenge for current machine learning systems. A weak form of out-of-distribution (OoD) generalization is the ability to successfully interpolate between multiple observed distributions. One way to achieve this is through robust optimization, which seeks to minimize the worst-case risk over convex combinations of the training distributions. However, a much stronger form of OoD generalization is the ability of models to extrapolate beyond the distributions observed during training. In pursuit of strong OoD generalization, we introduce the principle of Risk Extrapolation (REx). REx can be viewed as encouraging robustness over affine combinations of training risks, by encouraging strict equality between training risks. We show conceptually how this principle enables extrapolation, and demonstrate the effectiveness and scalability of instantiations of REx on various OoD generalization tasks. Our code can be found at https://github.com/capybaralet/REx_code_release.
Skip-Thought Memory Networks
Nov 24, 2015
Abstract:Question Answering (QA) is fundamental to natural language processing in that most nlp problems can be phrased as QA (Kumar et al., 2015). Current weakly supervised memory network models that have been proposed so far struggle at answering questions that involve relations among multiple entities (such as facebook's bAbi qa5-three-arg-relations in (Weston et al., 2015)). To address this problem of learning multi-argument multi-hop semantic relations for the purpose of QA, we propose a method that combines the jointly learned long-term read-write memory and attentive inference components of end-to-end memory networks (MemN2N) (Sukhbaatar et al., 2015) with distributed sentence vector representations encoded by a Skip-Thought model (Kiros et al., 2015). This choice to append Skip-Thought Vectors to the existing MemN2N framework is motivated by the fact that Skip-Thought Vectors have been shown to accurately model multi-argument semantic relations (Kiros et al., 2015).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge