Improving Meta-Learning Generalization with Activation-Based Early-Stopping

Meta-Learning algorithms for few-shot learning aim to train neural networks capable of generalizing to novel tasks using only a few examples. Early-stopping is critical for performance, halting model training when it reaches optimal generalization to the new task distribution. Early-stopping mechanisms in Meta-Learning typically rely on measuring the model performance on labeled examples from a meta-validation set drawn from the training (source) dataset. This is problematic in few-shot transfer learning settings, where the meta-test set comes from a different target dataset (OOD) and can potentially have a large distributional shift with the meta-validation set. In this work, we propose Activation Based Early-stopping (ABE), an alternative to using validation-based early-stopping for meta-learning. Specifically, we analyze the evolution, during meta-training, of the neural activations at each hidden layer, on a small set of unlabelled support examples from a single task of the target tasks distribution, as this constitutes a minimal and justifiably accessible information from the target problem. Our experiments show that simple, label agnostic statistics on the activations offer an effective way to estimate how the target generalization evolves over time. At each hidden layer, we characterize the activation distributions, from their first and second order moments, then further summarized along the feature dimensions, resulting in a compact yet intuitive characterization in a four-dimensional space. Detecting when, throughout training time, and at which layer, the target activation trajectory diverges from the activation trajectory of the source data, allows us to perform early-stopping and improve generalization in a large array of few-shot transfer learning settings, across different algorithms, source and target datasets.

Scaling Laws for the Few-Shot Adaptation of Pre-trained Image Classifiers

Empirical science of neural scaling laws is a rapidly growing area of significant importance to the future of machine learning, particularly in the light of recent breakthroughs achieved by large-scale pre-trained models such as GPT-3, CLIP and DALL-e. Accurately predicting the neural network performance with increasing resources such as data, compute and model size provides a more comprehensive evaluation of different approaches across multiple scales, as opposed to traditional point-wise comparisons of fixed-size models on fixed-size benchmarks, and, most importantly, allows for focus on the best-scaling, and thus most promising in the future, approaches. In this work, we consider a challenging problem of few-shot learning in image classification, especially when the target data distribution in the few-shot phase is different from the source, training, data distribution, in a sense that it includes new image classes not encountered during training. Our current main goal is to investigate how the amount of pre-training data affects the few-shot generalization performance of standard image classifiers. Our key observations are that (1) such performance improvements are well-approximated by power laws (linear log-log plots) as the training set size increases, (2) this applies to both cases of target data coming from either the same or from a different domain (i.e., new classes) as the training data, and (3) few-shot performance on new classes converges at a faster rate than the standard classification performance on previously seen classes. Our findings shed new light on the relationship between scale and generalization.

Towards Understanding Generalization in Gradient-Based Meta-Learning

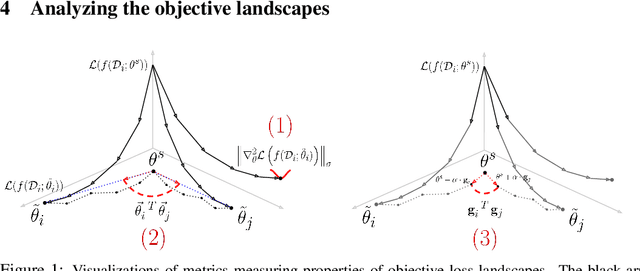
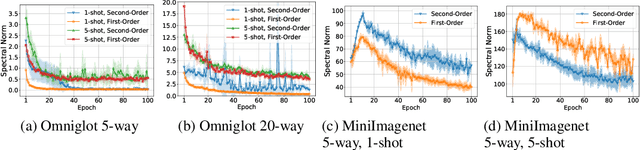
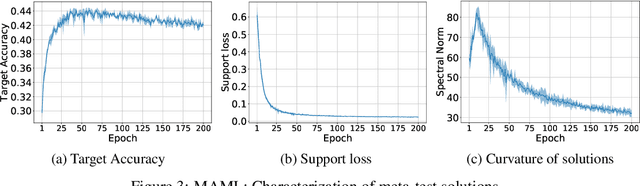
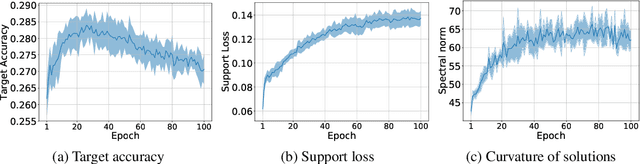
In this work we study generalization of neural networks in gradient-based meta-learning by analyzing various properties of the objective landscapes. We experimentally demonstrate that as meta-training progresses, the meta-test solutions, obtained after adapting the meta-train solution of the model, to new tasks via few steps of gradient-based fine-tuning, become flatter, lower in loss, and further away from the meta-train solution. We also show that those meta-test solutions become flatter even as generalization starts to degrade, thus providing an experimental evidence against the correlation between generalization and flat minima in the paradigm of gradient-based meta-leaning. Furthermore, we provide empirical evidence that generalization to new tasks is correlated with the coherence between their adaptation trajectories in parameter space, measured by the average cosine similarity between task-specific trajectory directions, starting from a same meta-train solution. We also show that coherence of meta-test gradients, measured by the average inner product between the task-specific gradient vectors evaluated at meta-train solution, is also correlated with generalization. Based on these observations, we propose a novel regularizer for MAML and provide experimental evidence for its effectiveness.