Tighter Confidence Bounds for Sequential Kernel Regression

Confidence bounds are an essential tool for rigorously quantifying the uncertainty of predictions. In this capacity, they can inform the exploration-exploitation trade-off and form a core component in many sequential learning and decision-making algorithms. Tighter confidence bounds give rise to algorithms with better empirical performance and better performance guarantees. In this work, we use martingale tail bounds and finite-dimensional reformulations of infinite-dimensional convex programs to establish new confidence bounds for sequential kernel regression. We prove that our new confidence bounds are always tighter than existing ones in this setting. We apply our confidence bounds to the kernel bandit problem, where future actions depend on the previous history. When our confidence bounds replace existing ones, the KernelUCB (GP-UCB) algorithm has better empirical performance, a matching worst-case performance guarantee and comparable computational cost. Our new confidence bounds can be used as a generic tool to design improved algorithms for other kernelised learning and decision-making problems.

Improved Algorithms for Stochastic Linear Bandits Using Tail Bounds for Martingale Mixtures

We present improved algorithms with worst-case regret guarantees for the stochastic linear bandit problem. The widely used "optimism in the face of uncertainty" principle reduces a stochastic bandit problem to the construction of a confidence sequence for the unknown reward function. The performance of the resulting bandit algorithm depends on the size of the confidence sequence, with smaller confidence sets yielding better empirical performance and stronger regret guarantees. In this work, we use a novel tail bound for adaptive martingale mixtures to construct confidence sequences which are suitable for stochastic bandits. These confidence sequences allow for efficient action selection via convex programming. We prove that a linear bandit algorithm based on our confidence sequences is guaranteed to achieve competitive worst-case regret. We show that our confidence sequences are tighter than competitors, both empirically and theoretically. Finally, we demonstrate that our tighter confidence sequences give improved performance in several hyperparameter tuning tasks.

PAC-Bayes Bounds for Bandit Problems: A Survey and Experimental Comparison

PAC-Bayes has recently re-emerged as an effective theory with which one can derive principled learning algorithms with tight performance guarantees. However, applications of PAC-Bayes to bandit problems are relatively rare, which is a great misfortune. Many decision-making problems in healthcare, finance and natural sciences can be modelled as bandit problems. In many of these applications, principled algorithms with strong performance guarantees would be very much appreciated. This survey provides an overview of PAC-Bayes performance bounds for bandit problems and an experimental comparison of these bounds. Our experimental comparison has revealed that available PAC-Bayes upper bounds on the cumulative regret are loose, whereas available PAC-Bayes lower bounds on the expected reward can be surprisingly tight. We found that an offline contextual bandit algorithm that learns a policy by optimising a PAC-Bayes bound was able to learn randomised neural network polices with competitive expected reward and non-vacuous performance guarantees.

PAC-Bayesian Lifelong Learning For Multi-Armed Bandits

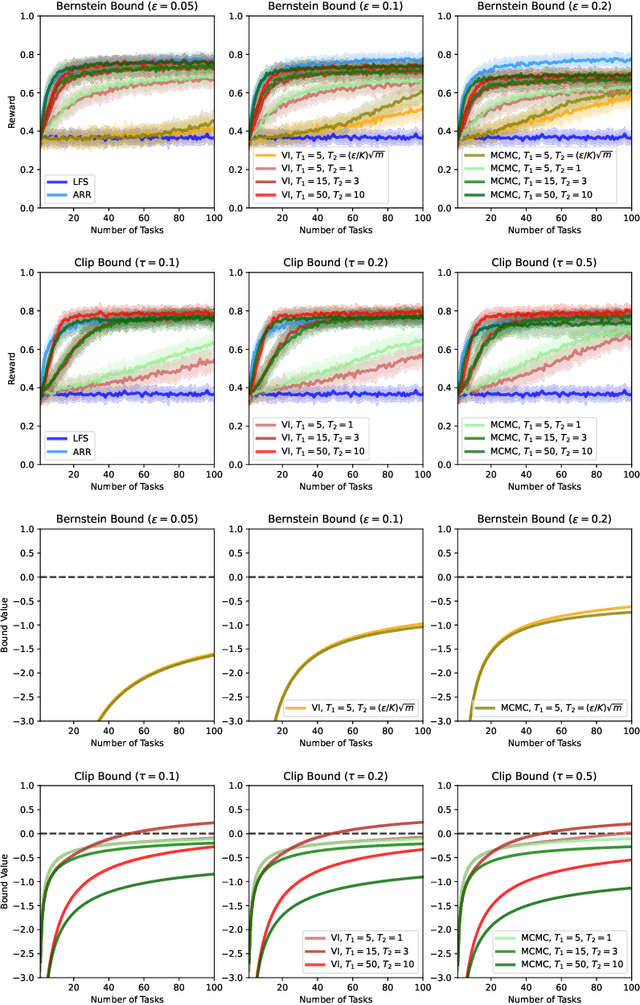
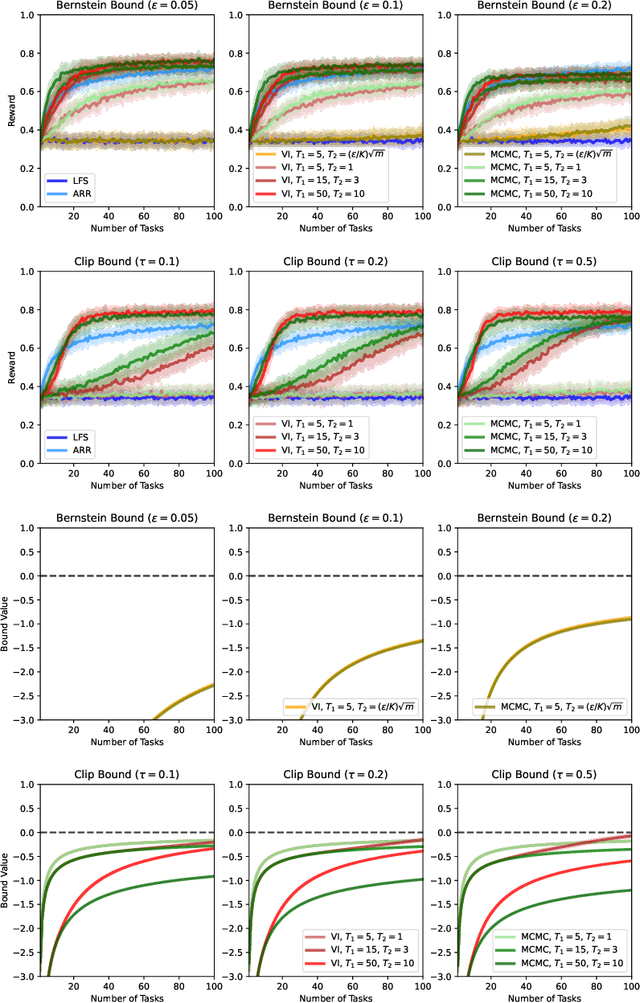
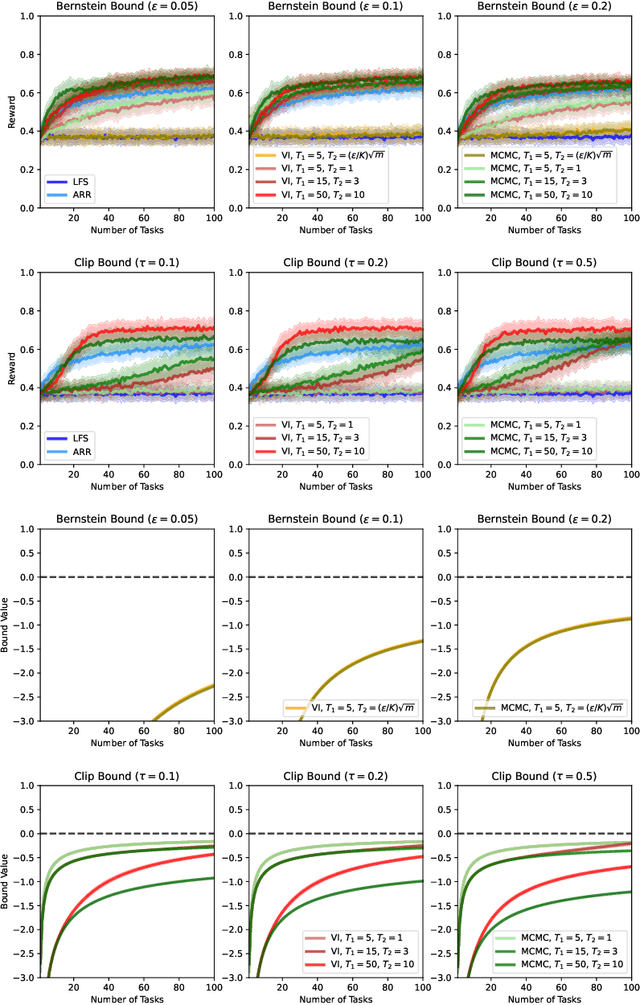
We present a PAC-Bayesian analysis of lifelong learning. In the lifelong learning problem, a sequence of learning tasks is observed one-at-a-time, and the goal is to transfer information acquired from previous tasks to new learning tasks. We consider the case when each learning task is a multi-armed bandit problem. We derive lower bounds on the expected average reward that would be obtained if a given multi-armed bandit algorithm was run in a new task with a particular prior and for a set number of steps. We propose lifelong learning algorithms that use our new bounds as learning objectives. Our proposed algorithms are evaluated in several lifelong multi-armed bandit problems and are found to perform better than a baseline method that does not use generalisation bounds.