PAC-Bayesian Lifelong Learning For Multi-Armed Bandits
Paper and Code
Mar 07, 2022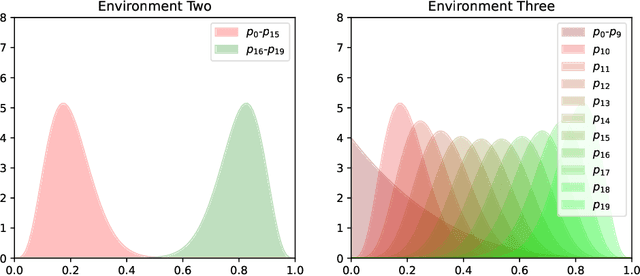
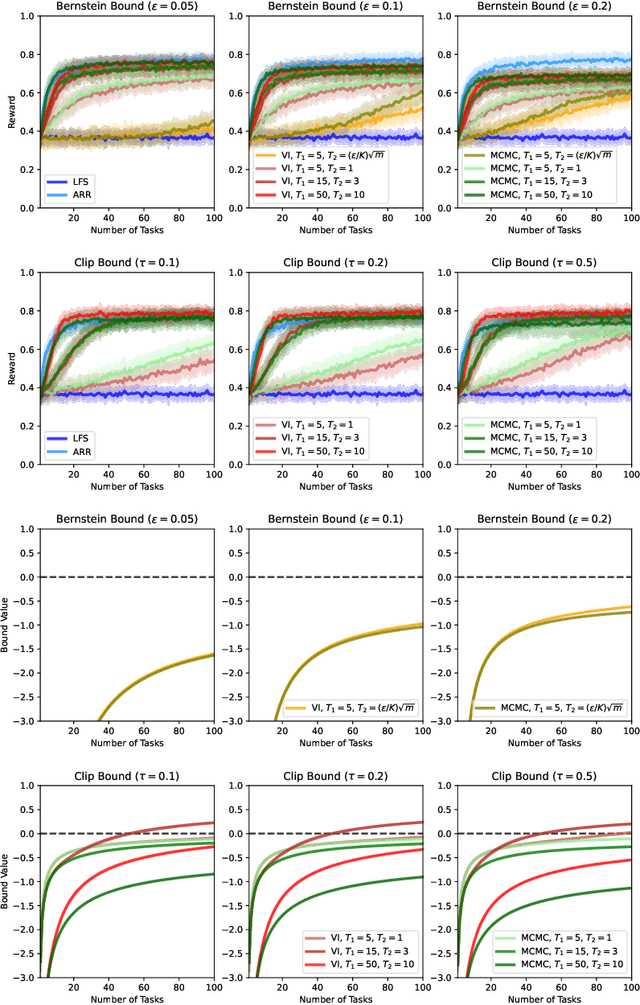
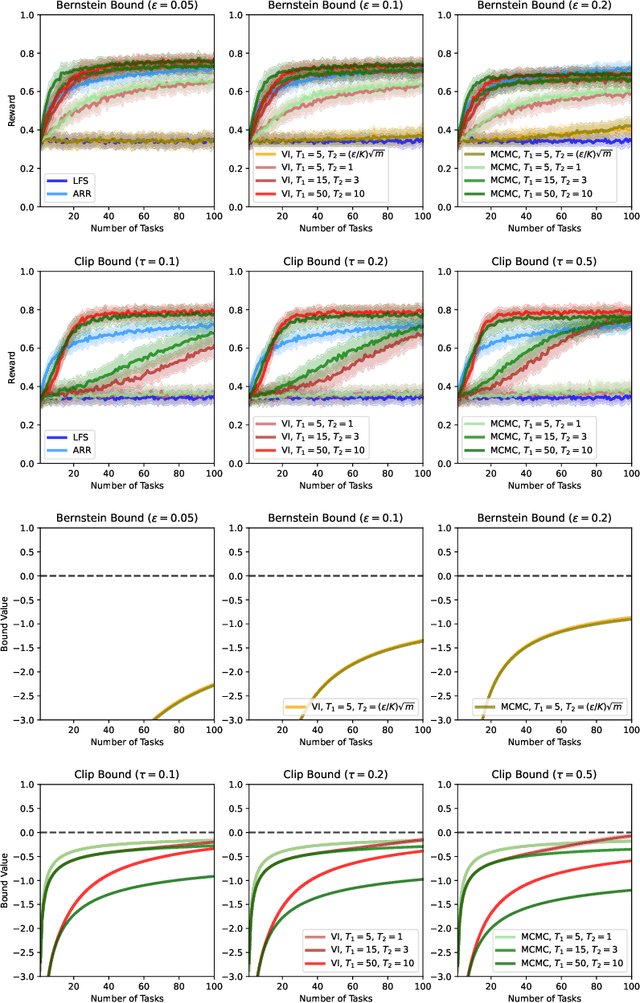
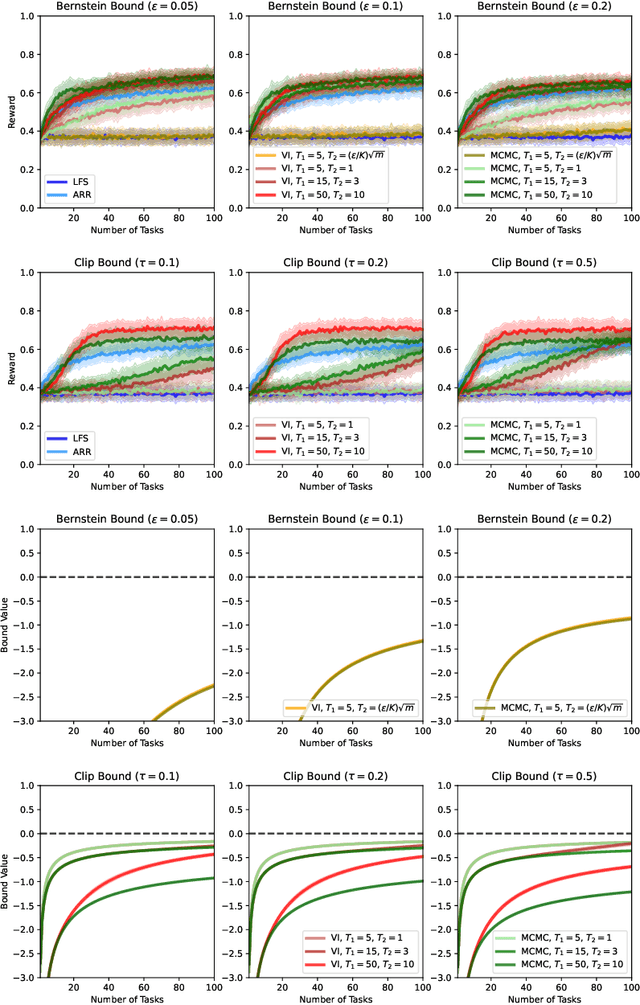
We present a PAC-Bayesian analysis of lifelong learning. In the lifelong learning problem, a sequence of learning tasks is observed one-at-a-time, and the goal is to transfer information acquired from previous tasks to new learning tasks. We consider the case when each learning task is a multi-armed bandit problem. We derive lower bounds on the expected average reward that would be obtained if a given multi-armed bandit algorithm was run in a new task with a particular prior and for a set number of steps. We propose lifelong learning algorithms that use our new bounds as learning objectives. Our proposed algorithms are evaluated in several lifelong multi-armed bandit problems and are found to perform better than a baseline method that does not use generalisation bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge