Tighter Confidence Bounds for Sequential Kernel Regression

Confidence bounds are an essential tool for rigorously quantifying the uncertainty of predictions. In this capacity, they can inform the exploration-exploitation trade-off and form a core component in many sequential learning and decision-making algorithms. Tighter confidence bounds give rise to algorithms with better empirical performance and better performance guarantees. In this work, we use martingale tail bounds and finite-dimensional reformulations of infinite-dimensional convex programs to establish new confidence bounds for sequential kernel regression. We prove that our new confidence bounds are always tighter than existing ones in this setting. We apply our confidence bounds to the kernel bandit problem, where future actions depend on the previous history. When our confidence bounds replace existing ones, the KernelUCB (GP-UCB) algorithm has better empirical performance, a matching worst-case performance guarantee and comparable computational cost. Our new confidence bounds can be used as a generic tool to design improved algorithms for other kernelised learning and decision-making problems.

Improved Algorithms for Stochastic Linear Bandits Using Tail Bounds for Martingale Mixtures

We present improved algorithms with worst-case regret guarantees for the stochastic linear bandit problem. The widely used "optimism in the face of uncertainty" principle reduces a stochastic bandit problem to the construction of a confidence sequence for the unknown reward function. The performance of the resulting bandit algorithm depends on the size of the confidence sequence, with smaller confidence sets yielding better empirical performance and stronger regret guarantees. In this work, we use a novel tail bound for adaptive martingale mixtures to construct confidence sequences which are suitable for stochastic bandits. These confidence sequences allow for efficient action selection via convex programming. We prove that a linear bandit algorithm based on our confidence sequences is guaranteed to achieve competitive worst-case regret. We show that our confidence sequences are tighter than competitors, both empirically and theoretically. Finally, we demonstrate that our tighter confidence sequences give improved performance in several hyperparameter tuning tasks.

PAC-Bayes Bounds for Bandit Problems: A Survey and Experimental Comparison

PAC-Bayes has recently re-emerged as an effective theory with which one can derive principled learning algorithms with tight performance guarantees. However, applications of PAC-Bayes to bandit problems are relatively rare, which is a great misfortune. Many decision-making problems in healthcare, finance and natural sciences can be modelled as bandit problems. In many of these applications, principled algorithms with strong performance guarantees would be very much appreciated. This survey provides an overview of PAC-Bayes performance bounds for bandit problems and an experimental comparison of these bounds. Our experimental comparison has revealed that available PAC-Bayes upper bounds on the cumulative regret are loose, whereas available PAC-Bayes lower bounds on the expected reward can be surprisingly tight. We found that an offline contextual bandit algorithm that learns a policy by optimising a PAC-Bayes bound was able to learn randomised neural network polices with competitive expected reward and non-vacuous performance guarantees.

Utilizing Expert Features for Contrastive Learning of Time-Series Representations

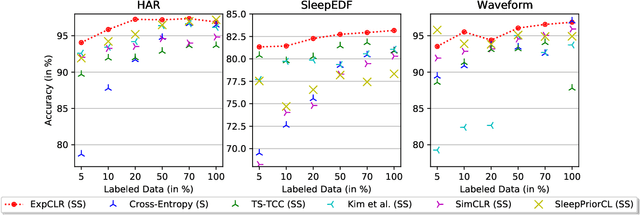
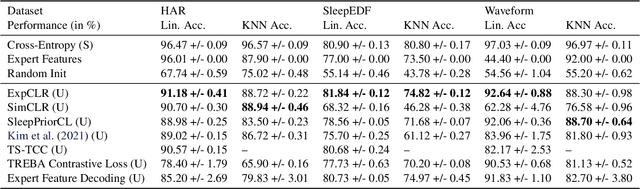
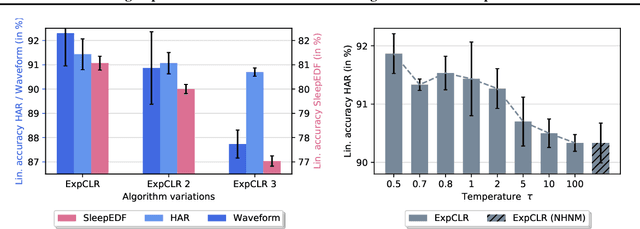
We present an approach that incorporates expert knowledge for time-series representation learning. Our method employs expert features to replace the commonly used data transformations in previous contrastive learning approaches. We do this since time-series data frequently stems from the industrial or medical field where expert features are often available from domain experts, while transformations are generally elusive for time-series data. We start by proposing two properties that useful time-series representations should fulfill and show that current representation learning approaches do not ensure these properties. We therefore devise ExpCLR, a novel contrastive learning approach built on an objective that utilizes expert features to encourage both properties for the learned representation. Finally, we demonstrate on three real-world time-series datasets that ExpCLR surpasses several state-of-the-art methods for both unsupervised and semi-supervised representation learning.

PAC-Bayesian Lifelong Learning For Multi-Armed Bandits

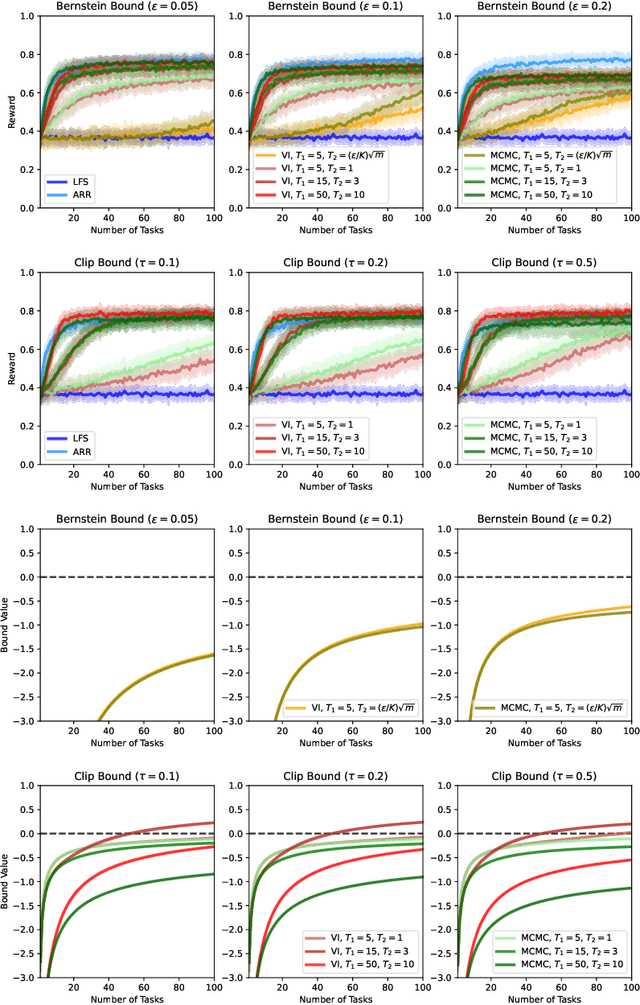
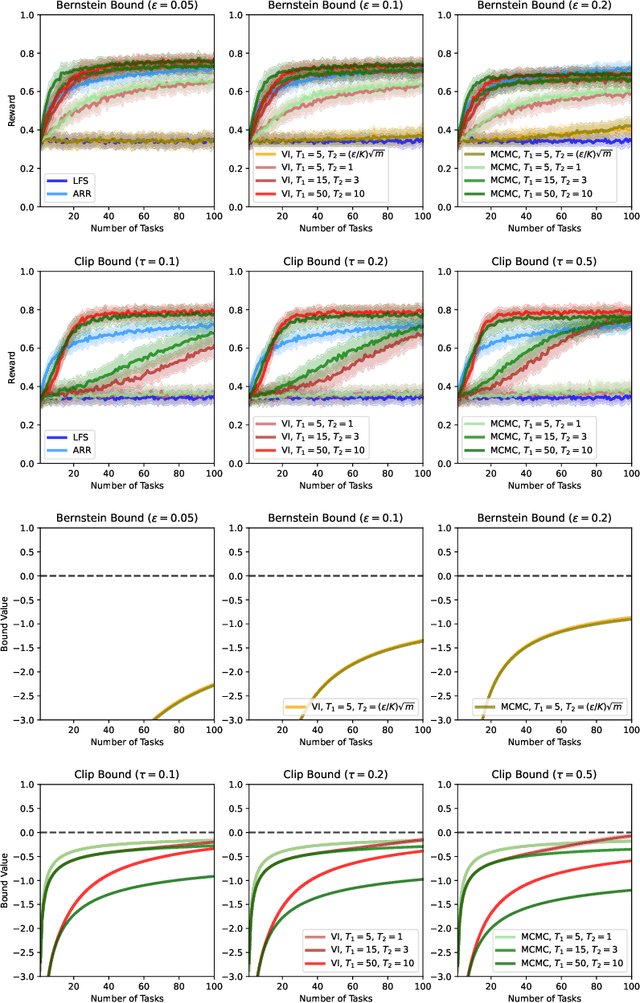
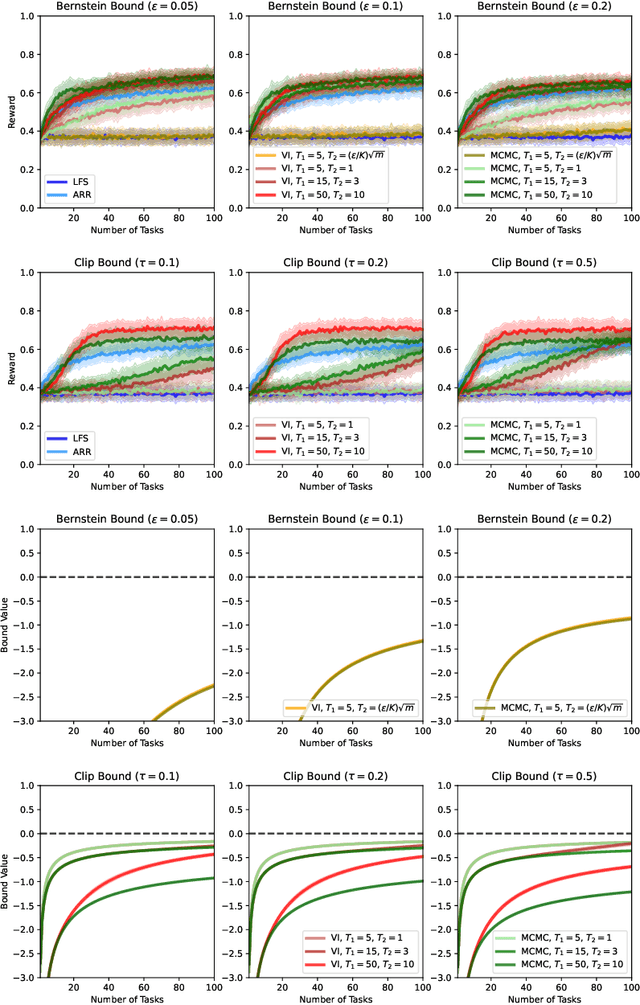
We present a PAC-Bayesian analysis of lifelong learning. In the lifelong learning problem, a sequence of learning tasks is observed one-at-a-time, and the goal is to transfer information acquired from previous tasks to new learning tasks. We consider the case when each learning task is a multi-armed bandit problem. We derive lower bounds on the expected average reward that would be obtained if a given multi-armed bandit algorithm was run in a new task with a particular prior and for a set number of steps. We propose lifelong learning algorithms that use our new bounds as learning objectives. Our proposed algorithms are evaluated in several lifelong multi-armed bandit problems and are found to perform better than a baseline method that does not use generalisation bounds.

SOSP: Efficiently Capturing Global Correlations by Second-Order Structured Pruning

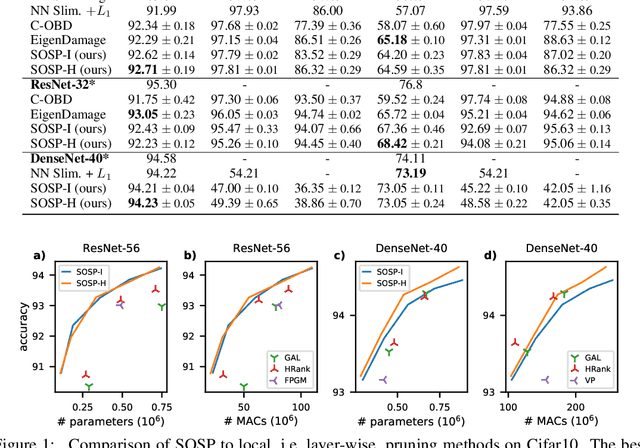
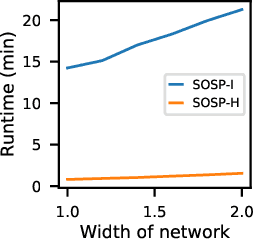
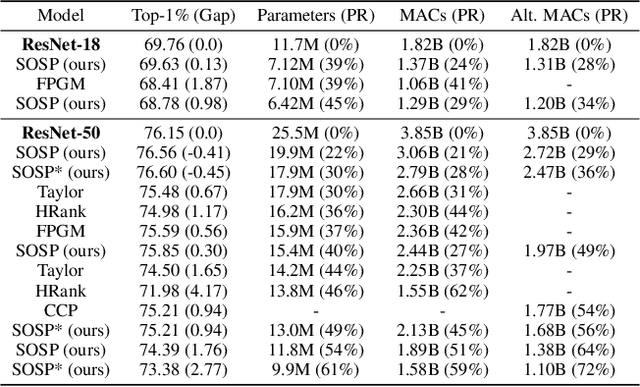
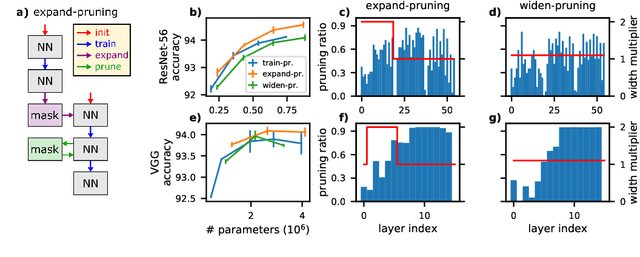
Pruning neural networks reduces inference time and memory costs. On standard hardware, these benefits will be especially prominent if coarse-grained structures, like feature maps, are pruned. We devise two novel saliency-based methods for second-order structured pruning (SOSP) which include correlations among all structures and layers. Our main method SOSP-H employs an innovative second-order approximation, which enables saliency evaluations by fast Hessian-vector products. SOSP-H thereby scales like a first-order method despite taking into account the full Hessian. We validate SOSP-H by comparing it to our second method SOSP-I that uses a well-established Hessian approximation, and to numerous state-of-the-art methods. While SOSP-H performs on par or better in terms of accuracy, it has clear advantages in terms of scalability and efficiency. This allowed us to scale SOSP-H to large-scale vision tasks, even though it captures correlations across all layers of the network. To underscore the global nature of our pruning methods, we evaluate their performance not only by removing structures from a pretrained network, but also by detecting architectural bottlenecks. We show that our algorithms allow to systematically reveal architectural bottlenecks, which we then remove to further increase the accuracy of the networks.

Which Minimizer Does My Neural Network Converge To?

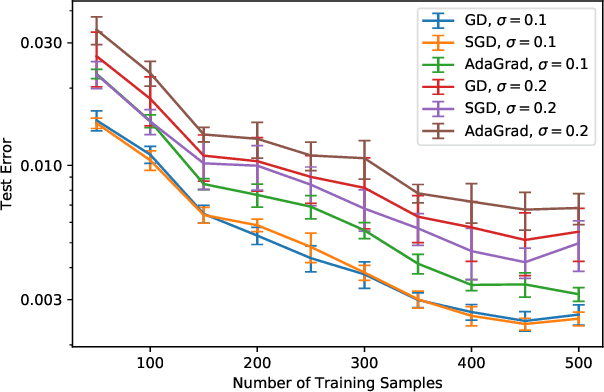
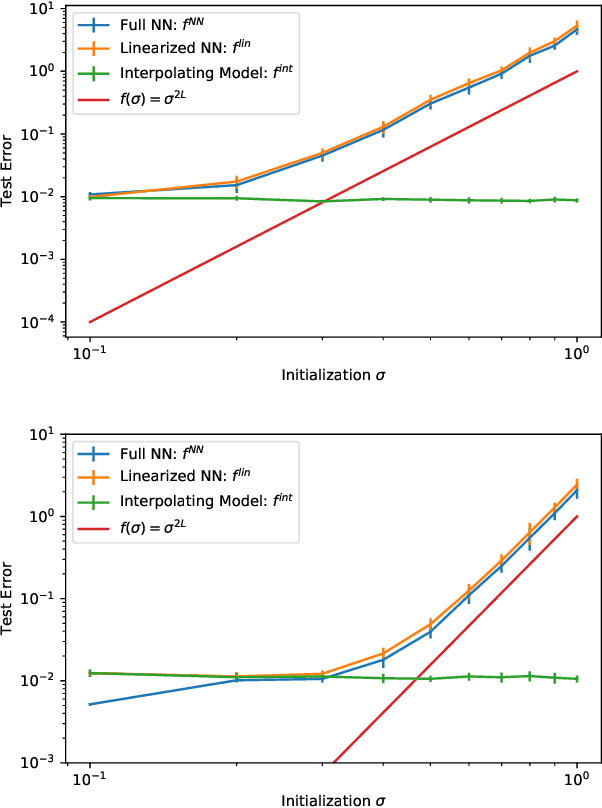
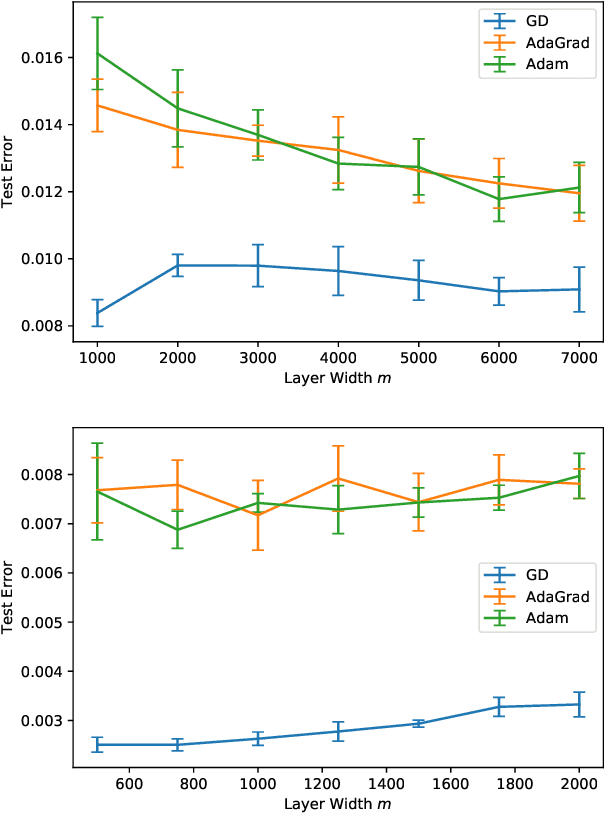
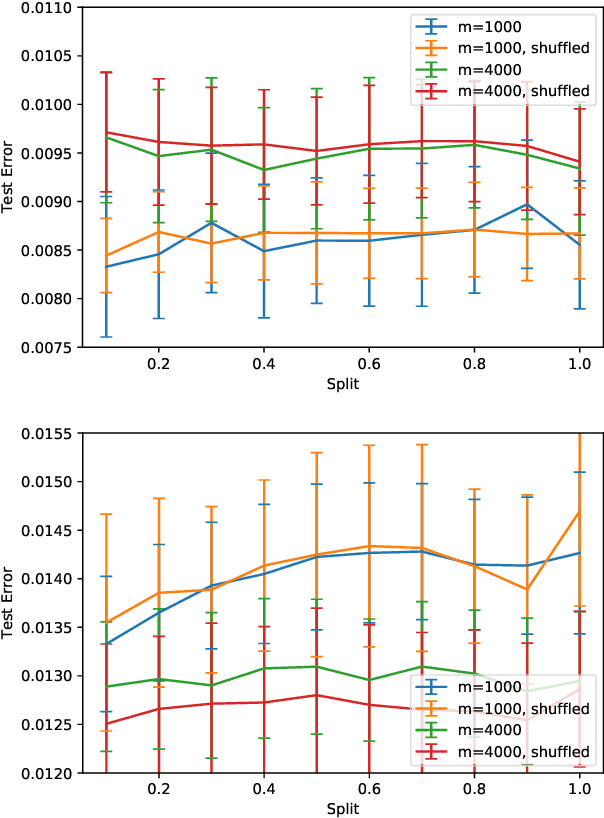
The loss surface of an overparameterized neural network (NN) possesses many global minima of zero training error. We explain how common variants of the standard NN training procedure change the minimizer obtained. First, we make explicit how the size of the initialization of a strongly overparameterized NN affects the minimizer and can deteriorate its final test performance. We propose a strategy to limit this effect. Then, we demonstrate that for adaptive optimization such as AdaGrad, the obtained minimizer generally differs from the gradient descent (GD) minimizer. This adaptive minimizer is changed further by stochastic mini-batch training, even though in the non-adaptive case GD and stochastic GD result in essentially the same minimizer. Lastly, we explain that these effects remain relevant for less overparameterized NNs. While overparameterization has its benefits, our work highlights that it induces sources of error absent from underparameterized models, some of which can be challenging to control.

Beyond the Mean-Field: Structured Deep Gaussian Processes Improve the Predictive Uncertainties

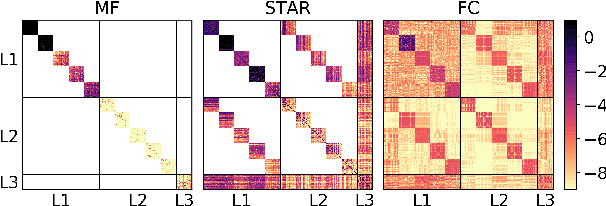
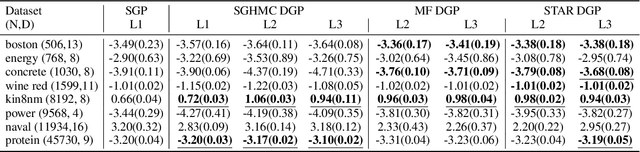
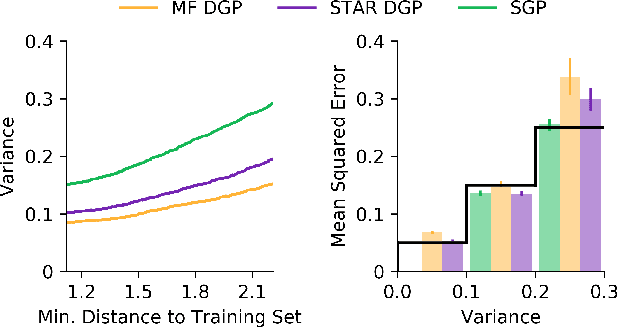
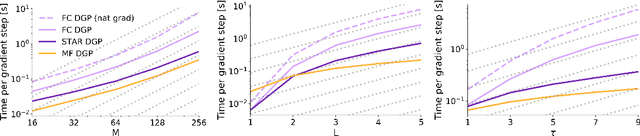
Deep Gaussian Processes learn probabilistic data representations for supervised learning by cascading multiple Gaussian Processes. While this model family promises flexible predictive distributions, exact inference is not tractable. Approximate inference techniques trade off the ability to closely resemble the posterior distribution against speed of convergence and computational efficiency. We propose a novel Gaussian variational family that allows for retaining covariances between latent processes while achieving fast convergence by marginalising out all global latent variables. After providing a proof of how this marginalisation can be done for general covariances, we restrict them to the ones we empirically found to be most important in order to also achieve computational efficiency. We provide an efficient implementation of our new approach and apply it to several regression benchmark datasets. We find that it yields more accurate predictive distributions, in particular for test data points that are distant from the training set.

Learning Gaussian Processes by Minimizing PAC-Bayesian Generalization Bounds

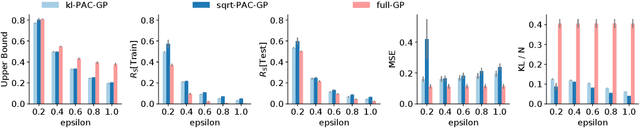
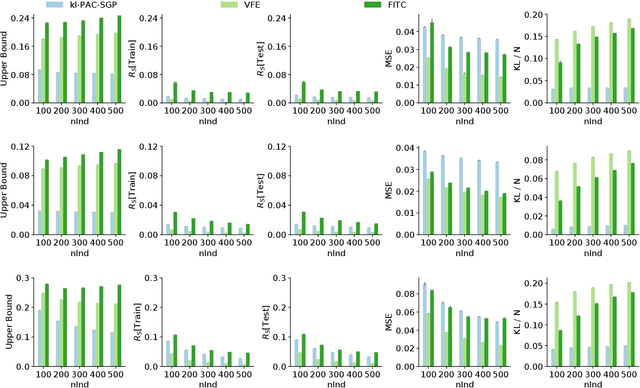
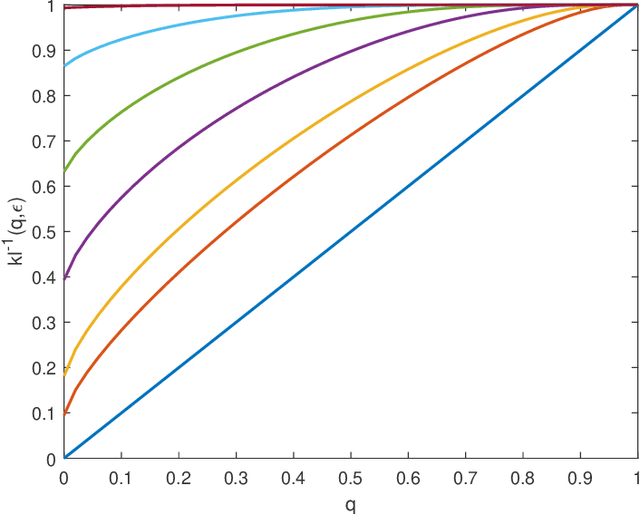
Gaussian Processes (GPs) are a generic modelling tool for supervised learning. While they have been successfully applied on large datasets, their use in safety-critical applications is hindered by the lack of good performance guarantees. To this end, we propose a method to learn GPs and their sparse approximations by directly optimizing a PAC-Bayesian bound on their generalization performance, instead of maximizing the marginal likelihood. Besides its theoretical appeal, we find in our evaluation that our learning method is robust and yields significantly better generalization guarantees than other common GP approaches on several regression benchmark datasets.