Traversing Time with Multi-Resolution Gaussian Process State-Space Models

Gaussian Process state-space models capture complex temporal dependencies in a principled manner by placing a Gaussian Process prior on the transition function. These models have a natural interpretation as discretized stochastic differential equations, but inference for long sequences with fast and slow transitions is difficult. Fast transitions need tight discretizations whereas slow transitions require backpropagating the gradients over long subtrajectories. We propose a novel Gaussian process state-space architecture composed of multiple components, each trained on a different resolution, to model effects on different timescales. The combined model allows traversing time on adaptive scales, providing efficient inference for arbitrarily long sequences with complex dynamics. We benchmark our novel method on semi-synthetic data and on an engine modeling task. In both experiments, our approach compares favorably against its state-of-the-art alternatives that operate on a single time-scale only.

Beyond the Mean-Field: Structured Deep Gaussian Processes Improve the Predictive Uncertainties

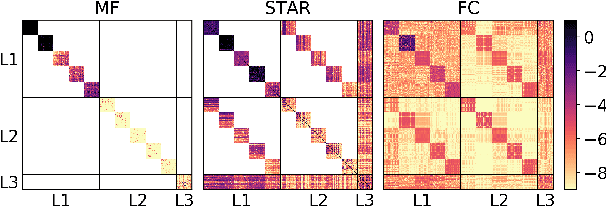
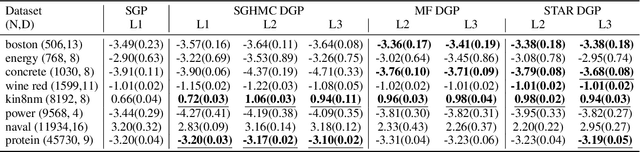
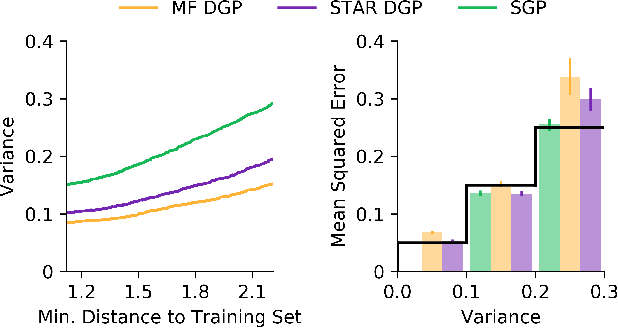
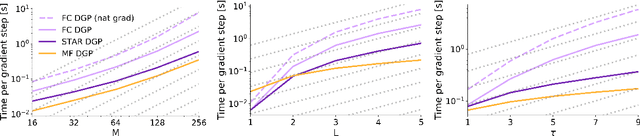
Deep Gaussian Processes learn probabilistic data representations for supervised learning by cascading multiple Gaussian Processes. While this model family promises flexible predictive distributions, exact inference is not tractable. Approximate inference techniques trade off the ability to closely resemble the posterior distribution against speed of convergence and computational efficiency. We propose a novel Gaussian variational family that allows for retaining covariances between latent processes while achieving fast convergence by marginalising out all global latent variables. After providing a proof of how this marginalisation can be done for general covariances, we restrict them to the ones we empirically found to be most important in order to also achieve computational efficiency. We provide an efficient implementation of our new approach and apply it to several regression benchmark datasets. We find that it yields more accurate predictive distributions, in particular for test data points that are distant from the training set.