Global Safe Sequential Learning via Efficient Knowledge Transfer

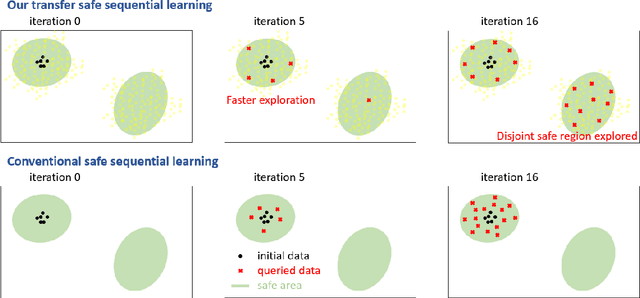
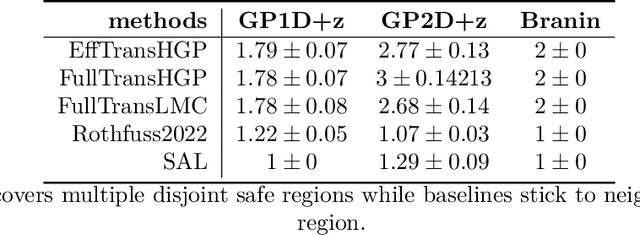
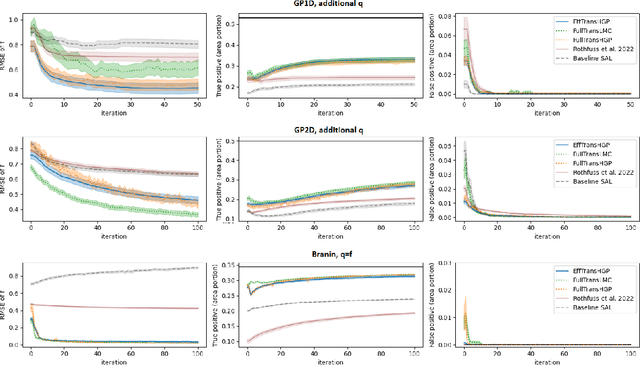
Sequential learning methods such as active learning and Bayesian optimization select the most informative data to learn about a task. In many medical or engineering applications, the data selection is constrained by a priori unknown safety conditions. A promissing line of safe learning methods utilize Gaussian processes (GPs) to model the safety probability and perform data selection in areas with high safety confidence. However, accurate safety modeling requires prior knowledge or consumes data. In addition, the safety confidence centers around the given observations which leads to local exploration. As transferable source knowledge is often available in safety critical experiments, we propose to consider transfer safe sequential learning to accelerate the learning of safety. We further consider a pre-computation of source components to reduce the additional computational load that is introduced by incorporating source data. In this paper, we theoretically analyze the maximum explorable safe regions of conventional safe learning methods. Furthermore, we empirically demonstrate that our approach 1) learns a task with lower data consumption, 2) globally explores multiple disjoint safe regions under guidance of the source knowledge, and 3) operates with computation comparable to conventional safe learning methods.

Traversing Time with Multi-Resolution Gaussian Process State-Space Models

Gaussian Process state-space models capture complex temporal dependencies in a principled manner by placing a Gaussian Process prior on the transition function. These models have a natural interpretation as discretized stochastic differential equations, but inference for long sequences with fast and slow transitions is difficult. Fast transitions need tight discretizations whereas slow transitions require backpropagating the gradients over long subtrajectories. We propose a novel Gaussian process state-space architecture composed of multiple components, each trained on a different resolution, to model effects on different timescales. The combined model allows traversing time on adaptive scales, providing efficient inference for arbitrarily long sequences with complex dynamics. We benchmark our novel method on semi-synthetic data and on an engine modeling task. In both experiments, our approach compares favorably against its state-of-the-art alternatives that operate on a single time-scale only.