Safe Active Learning for Gaussian Differential Equations

Gaussian Process differential equations (GPODE) have recently gained momentum due to their ability to capture dynamics behavior of systems and also represent uncertainty in predictions. Prior work has described the process of training the hyperparameters and, thereby, calibrating GPODE to data. How to design efficient algorithms to collect data for training GPODE models is still an open field of research. Nevertheless high-quality training data is key for model performance. Furthermore, data collection leads to time-cost and financial-cost and might in some areas even be safety critical to the system under test. Therefore, algorithms for safe and efficient data collection are central for building high quality GPODE models. Our novel Safe Active Learning (SAL) for GPODE algorithm addresses this challenge by suggesting a mechanism to propose efficient and non-safety-critical data to collect. SAL GPODE does so by sequentially suggesting new data, measuring it and updating the GPODE model with the new data. In this way, subsequent data points are iteratively suggested. The core of our SAL GPODE algorithm is a constrained optimization problem maximizing information of new data for GPODE model training constrained by the safety of the underlying system. We demonstrate our novel SAL GPODE's superiority compared to a standard, non-active way of measuring new data on two relevant examples.

Batch Active Learning in Gaussian Process Regression using Derivatives

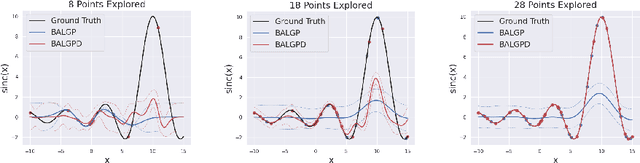
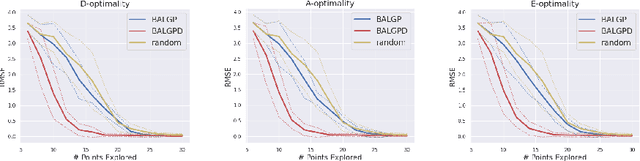
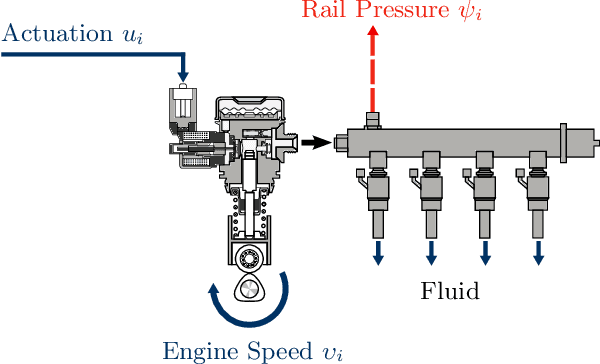
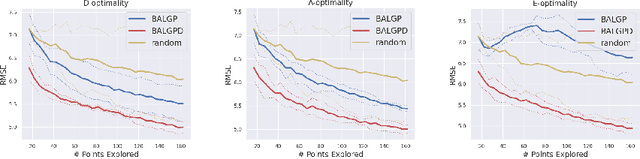
We investigate the use of derivative information for Batch Active Learning in Gaussian Process regression models. The proposed approach employs the predictive covariance matrix for selection of data batches to exploit full correlation of samples. We theoretically analyse our proposed algorithm taking different optimality criteria into consideration and provide empirical comparisons highlighting the advantage of incorporating derivatives information. Our results show the effectiveness of our approach across diverse applications.

Amortized Active Learning for Nonparametric Functions

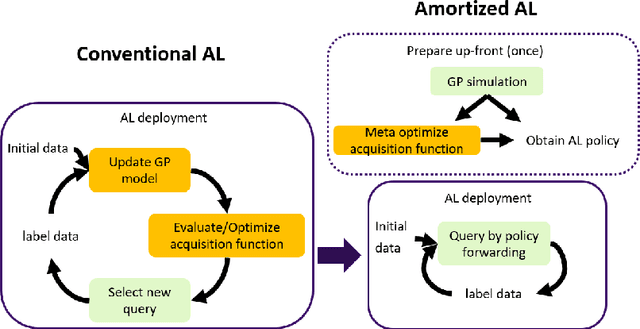
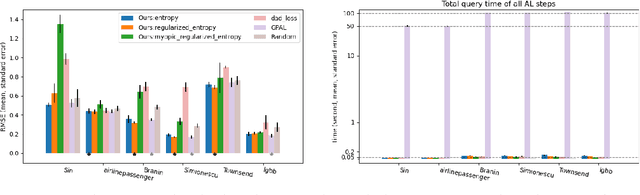
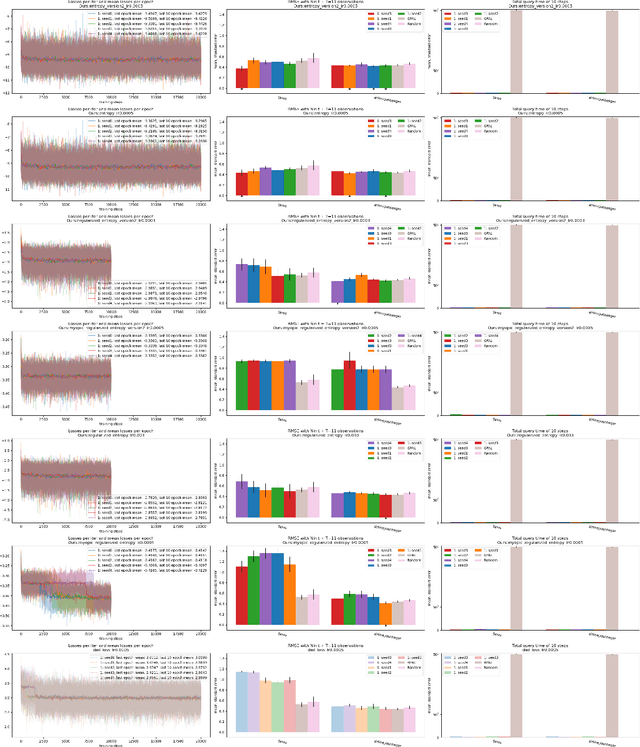
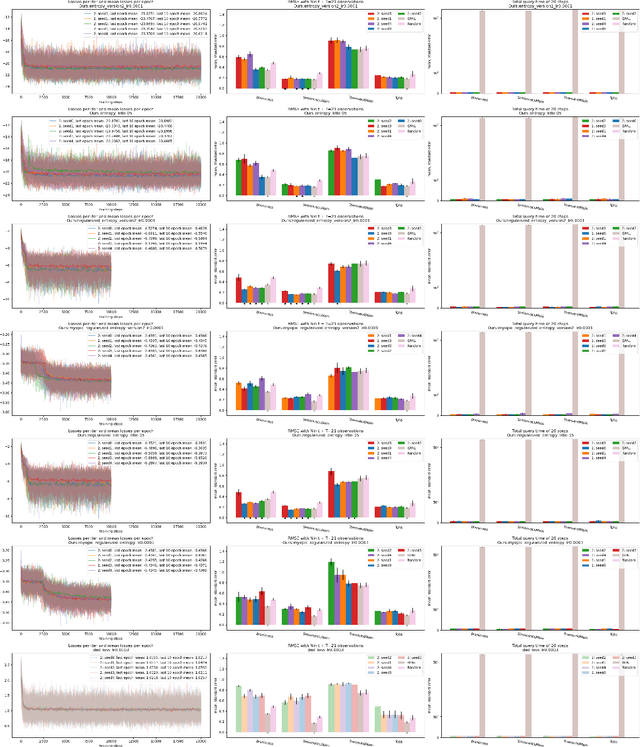
Active learning (AL) is a sequential learning scheme aiming to select the most informative data. AL reduces data consumption and avoids the cost of labeling large amounts of data. However, AL trains the model and solves an acquisition optimization for each selection. It becomes expensive when the model training or acquisition optimization is challenging. In this paper, we focus on active nonparametric function learning, where the gold standard Gaussian process (GP) approaches suffer from cubic time complexity. We propose an amortized AL method, where new data are suggested by a neural network which is trained up-front without any real data (Figure 1). Our method avoids repeated model training and requires no acquisition optimization during the AL deployment. We (i) utilize GPs as function priors to construct an AL simulator, (ii) train an AL policy that can zero-shot generalize from simulation to real learning problems of nonparametric functions and (iii) achieve real-time data selection and comparable learning performances to time-consuming baseline methods.

Future Aware Safe Active Learning of Time Varying Systems using Gaussian Processes

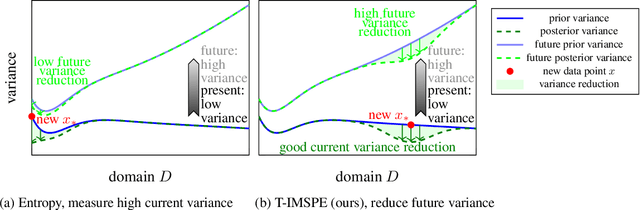
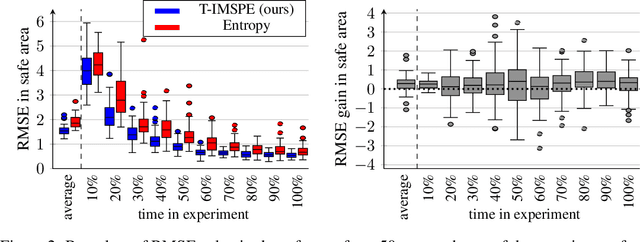
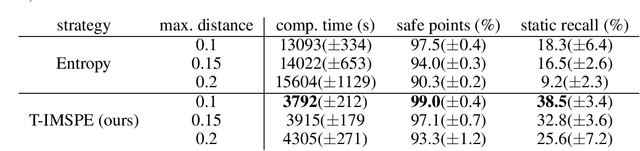
Experimental exploration of high-cost systems with safety constraints, common in engineering applications, is a challenging endeavor. Data-driven models offer a promising solution, but acquiring the requisite data remains expensive and is potentially unsafe. Safe active learning techniques prove essential, enabling the learning of high-quality models with minimal expensive data points and high safety. This paper introduces a safe active learning framework tailored for time-varying systems, addressing drift, seasonal changes, and complexities due to dynamic behavior. The proposed Time-aware Integrated Mean Squared Prediction Error (T-IMSPE) method minimizes posterior variance over current and future states, optimizing information gathering also in the time domain. Empirical results highlight T-IMSPE's advantages in model quality through toy and real-world examples. State of the art Gaussian processes are compatible with T-IMSPE. Our theoretical contributions include a clear delineation which Gaussian process kernels, domains, and weighting measures are suitable for T-IMSPE and even beyond for its non-time aware predecessor IMSPE.

Efficiently Computable Safety Bounds for Gaussian Processes in Active Learning

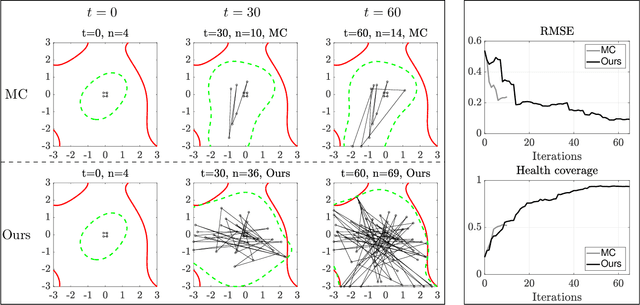
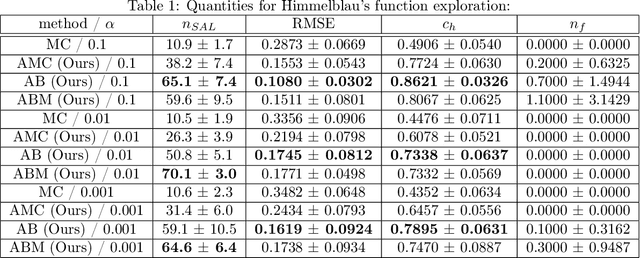
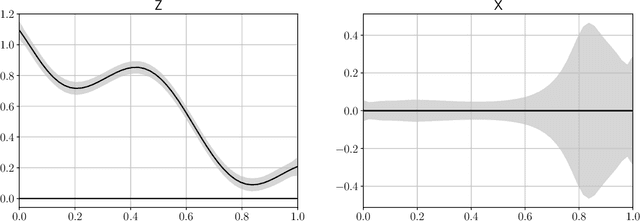
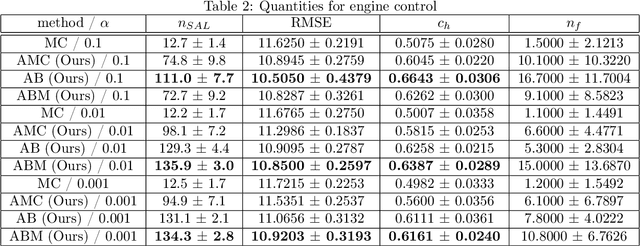
Active learning of physical systems must commonly respect practical safety constraints, which restricts the exploration of the design space. Gaussian Processes (GPs) and their calibrated uncertainty estimations are widely used for this purpose. In many technical applications the design space is explored via continuous trajectories, along which the safety needs to be assessed. This is particularly challenging for strict safety requirements in GP methods, as it employs computationally expensive Monte-Carlo sampling of high quantiles. We address these challenges by providing provable safety bounds based on the adaptively sampled median of the supremum of the posterior GP. Our method significantly reduces the number of samples required for estimating high safety probabilities, resulting in faster evaluation without sacrificing accuracy and exploration speed. The effectiveness of our safe active learning approach is demonstrated through extensive simulations and validated using a real-world engine example.

Global Safe Sequential Learning via Efficient Knowledge Transfer

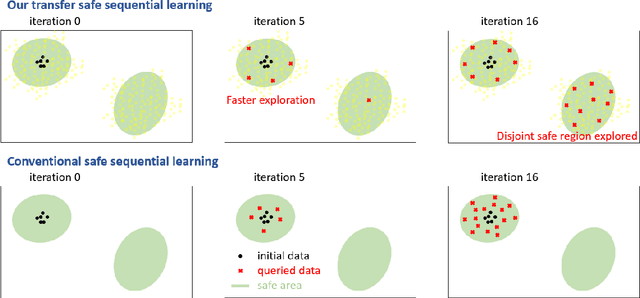
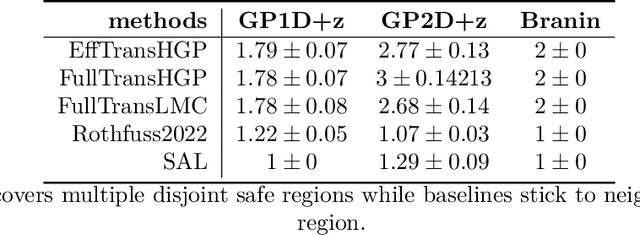
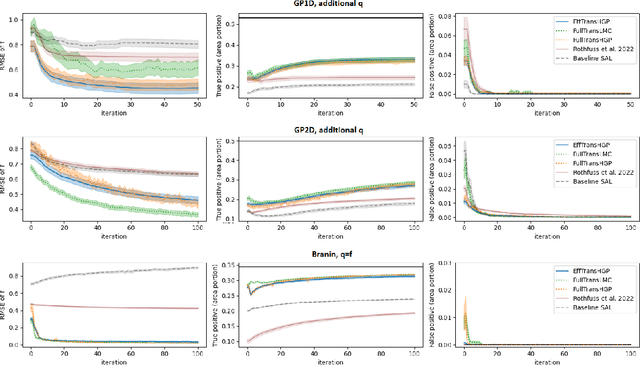
Sequential learning methods such as active learning and Bayesian optimization select the most informative data to learn about a task. In many medical or engineering applications, the data selection is constrained by a priori unknown safety conditions. A promissing line of safe learning methods utilize Gaussian processes (GPs) to model the safety probability and perform data selection in areas with high safety confidence. However, accurate safety modeling requires prior knowledge or consumes data. In addition, the safety confidence centers around the given observations which leads to local exploration. As transferable source knowledge is often available in safety critical experiments, we propose to consider transfer safe sequential learning to accelerate the learning of safety. We further consider a pre-computation of source components to reduce the additional computational load that is introduced by incorporating source data. In this paper, we theoretically analyze the maximum explorable safe regions of conventional safe learning methods. Furthermore, we empirically demonstrate that our approach 1) learns a task with lower data consumption, 2) globally explores multiple disjoint safe regions under guidance of the source knowledge, and 3) operates with computation comparable to conventional safe learning methods.

Safe Active Learning for Time-Series Modeling with Gaussian Processes

Learning time-series models is useful for many applications, such as simulation and forecasting. In this study, we consider the problem of actively learning time-series models while taking given safety constraints into account. For time-series modeling we employ a Gaussian process with a nonlinear exogenous input structure. The proposed approach generates data appropriate for time series model learning, i.e. input and output trajectories, by dynamically exploring the input space. The approach parametrizes the input trajectory as consecutive trajectory sections, which are determined stepwise given safety requirements and past observations. We analyze the proposed algorithm and evaluate it empirically on a technical application. The results show the effectiveness of our approach in a realistic technical use case.

Amortized Inference for Gaussian Process Hyperparameters of Structured Kernels

Learning the kernel parameters for Gaussian processes is often the computational bottleneck in applications such as online learning, Bayesian optimization, or active learning. Amortizing parameter inference over different datasets is a promising approach to dramatically speed up training time. However, existing methods restrict the amortized inference procedure to a fixed kernel structure. The amortization network must be redesigned manually and trained again in case a different kernel is employed, which leads to a large overhead in design time and training time. We propose amortizing kernel parameter inference over a complete kernel-structure-family rather than a fixed kernel structure. We do that via defining an amortization network over pairs of datasets and kernel structures. This enables fast kernel inference for each element in the kernel family without retraining the amortization network. As a by-product, our amortization network is able to do fast ensembling over kernel structures. In our experiments, we show drastically reduced inference time combined with competitive test performance for a large set of kernels and datasets.

Hierarchical-Hyperplane Kernels for Actively Learning Gaussian Process Models of Nonstationary Systems

Learning precise surrogate models of complex computer simulations and physical machines often require long-lasting or expensive experiments. Furthermore, the modeled physical dependencies exhibit nonlinear and nonstationary behavior. Machine learning methods that are used to produce the surrogate model should therefore address these problems by providing a scheme to keep the number of queries small, e.g. by using active learning and be able to capture the nonlinear and nonstationary properties of the system. One way of modeling the nonstationarity is to induce input-partitioning, a principle that has proven to be advantageous in active learning for Gaussian processes. However, these methods either assume a known partitioning, need to introduce complex sampling schemes or rely on very simple geometries. In this work, we present a simple, yet powerful kernel family that incorporates a partitioning that: i) is learnable via gradient-based methods, ii) uses a geometry that is more flexible than previous ones, while still being applicable in the low data regime. Thus, it provides a good prior for active learning procedures. We empirically demonstrate excellent performance on various active learning tasks.

Safe Active Learning for Multi-Output Gaussian Processes

Multi-output regression problems are commonly encountered in science and engineering. In particular, multi-output Gaussian processes have been emerged as a promising tool for modeling these complex systems since they can exploit the inherent correlations and provide reliable uncertainty estimates. In many applications, however, acquiring the data is expensive and safety concerns might arise (e.g. robotics, engineering). We propose a safe active learning approach for multi-output Gaussian process regression. This approach queries the most informative data or output taking the relatedness between the regressors and safety constraints into account. We prove the effectiveness of our approach by providing theoretical analysis and by demonstrating empirical results on simulated datasets and on a real-world engineering dataset. On all datasets, our approach shows improved convergence compared to its competitors.