Efficiently Computable Safety Bounds for Gaussian Processes in Active Learning

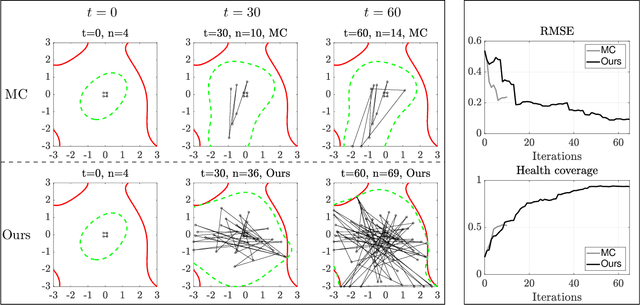
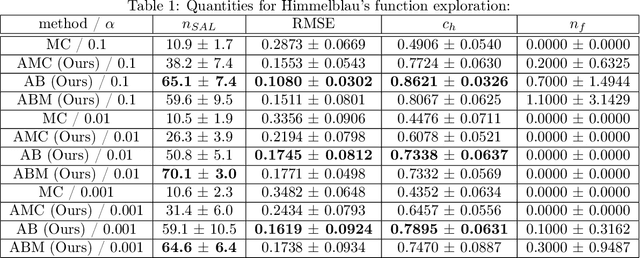
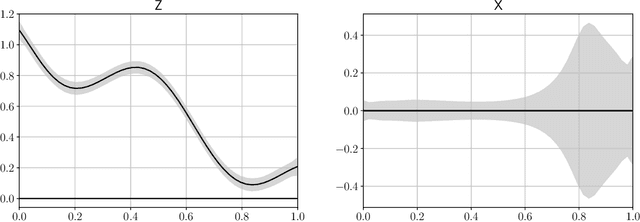
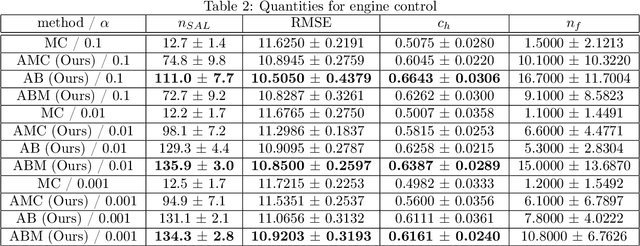
Active learning of physical systems must commonly respect practical safety constraints, which restricts the exploration of the design space. Gaussian Processes (GPs) and their calibrated uncertainty estimations are widely used for this purpose. In many technical applications the design space is explored via continuous trajectories, along which the safety needs to be assessed. This is particularly challenging for strict safety requirements in GP methods, as it employs computationally expensive Monte-Carlo sampling of high quantiles. We address these challenges by providing provable safety bounds based on the adaptively sampled median of the supremum of the posterior GP. Our method significantly reduces the number of samples required for estimating high safety probabilities, resulting in faster evaluation without sacrificing accuracy and exploration speed. The effectiveness of our safe active learning approach is demonstrated through extensive simulations and validated using a real-world engine example.

On Extreme Value Asymptotics of Projected Sample Covariances in High Dimensions with Applications in Finance and Convolutional Networks

Maximum-type statistics of certain functions of the sample covariance matrix of high-dimensional vector time series are studied to statistically confirm or reject the null hypothesis that a data set has been collected under normal conditions. The approach generalizes the case of the maximal deviation of the sample autocovariances function from its assumed values. Within a linear time series framework it is shown that Gumbel-type extreme value asymptotics holds true. As applications we discuss long-only mimimal-variance portfolio optimization and subportfolio analysis with respect to idiosyncratic risks, ETF index tracking by sparse tracking portfolios, convolutional deep learners for image analysis and the analysis of array-of-sensors data.

Online Detection of Changes in Moment-Based Projections: When to Retrain Deep Learners or Update Portfolios?

Sequential monitoring of high-dimensional nonlinear time series is studied for a projection of the second-moment matrix, a problem interesting in its own right and specifically arising in finance and deep learning. Open-end as well as closed-end monitoring is studied under mild assumptions on the training sample and the observations of the monitoring period. Asymptotics is based on Gaussian approximations of projected partial sums allowing for an estimated projection vector. Estimation is studied both for classical non-$\ell_0$-sparsity as well as under sparsity. For the case that the optimal projection depends on the unknown covariance matrix, hard- and soft-thresholded estimators are studied. Applications in finance and training of deep neural networks are discussed. The proposed detectors typically allow to reduce dramatically the required computational costs as illustrated by monitoring synthetic data.

Cross-Validation and Uncertainty Determination for Randomized Neural Networks with Applications to Mobile Sensors

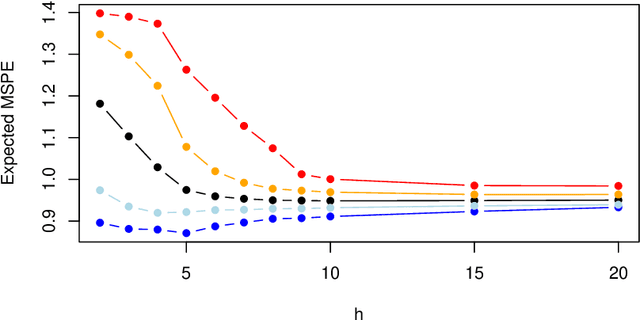
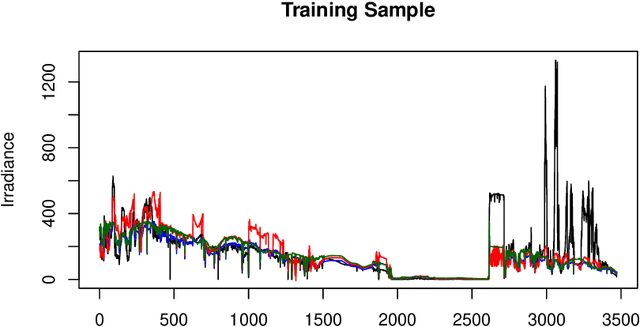
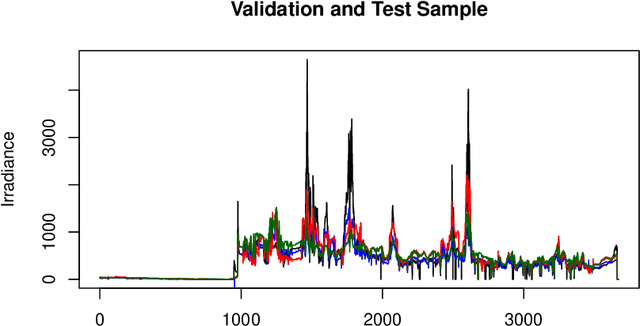
Randomized artificial neural networks such as extreme learning machines provide an attractive and efficient method for supervised learning under limited computing ressources and green machine learning. This especially applies when equipping mobile devices (sensors) with weak artificial intelligence. Results are discussed about supervised learning with such networks and regression methods in terms of consistency and bounds for the generalization and prediction error. Especially, some recent results are reviewed addressing learning with data sampled by moving sensors leading to non-stationary and dependent samples. As randomized networks lead to random out-of-sample performance measures, we study a cross-validation approach to handle the randomness and make use of it to improve out-of-sample performance. Additionally, a computationally efficient approach to determine the resulting uncertainty in terms of a confidence interval for the mean out-of-sample prediction error is discussed based on two-stage estimation. The approach is applied to a prediction problem arising in vehicle integrated photovoltaics.

Is there a role for statistics in artificial intelligence?

The research on and application of artificial intelligence (AI) has triggered a comprehensive scientific, economic, social and political discussion. Here we argue that statistics, as an interdisciplinary scientific field, plays a substantial role both for the theoretical and practical understanding of AI and for its future development. Statistics might even be considered a core element of AI. With its specialist knowledge of data evaluation, starting with the precise formulation of the research question and passing through a study design stage on to analysis and interpretation of the results, statistics is a natural partner for other disciplines in teaching, research and practice. This paper aims at contributing to the current discussion by highlighting the relevance of statistical methodology in the context of AI development. In particular, we discuss contributions of statistics to the field of artificial intelligence concerning methodological development, planning and design of studies, assessment of data quality and data collection, differentiation of causality and associations and assessment of uncertainty in results. Moreover, the paper also deals with the equally necessary and meaningful extension of curricula in schools and universities.

Extreme Learning and Regression for Objects Moving in Non-Stationary Spatial Environments

We study supervised learning by extreme learning machines and regression for autonomous objects moving in a non-stationary spatial environment. In general, this results in non-stationary data in contrast to the i.i.d. sampling typically studied in learning theory. The stochastic model for the environment and data collection especially allows for algebraically decaying weak dependence and spatial heterogeneity, for example induced by interactions of the object with sources of randomness spread over the spatial domain. Both least squares and ridge learning as a computationally cheap regularization method is studied. Consistency and asymptotic normality of the least squares and ridge regression estimates is shown under weak conditions. The results also cover consistency in terms of bounds for the sample squared predicition error. Lastly, we discuss a resampling method to compute confidence regions.

Automatic Processing and Solar Cell Detection in Photovoltaic Electroluminescence Images

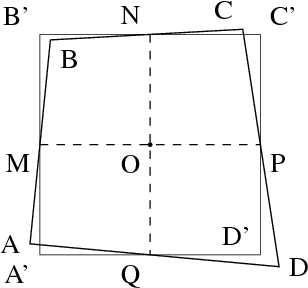
Electroluminescence (EL) imaging is a powerful and established technique for assessing the quality of photovoltaic (PV) modules, which consist of many electrically connected solar cells arranged in a grid. The analysis of imperfect real-world images requires reliable methods for preprocessing, detection and extraction of the cells. We propose several methods for those tasks, which, however, can be modified to related imaging problems where similar geometric objects need to be detected accurately. Allowing for images taken under difficult outdoor conditions, we present methods to correct for rotation and perspective distortions. The next important step is the extraction of the solar cells of a PV module, for instance to pass them to a procedure to detect and analyze defects on their surface. We propose a method based on specialized Hough transforms, which allows to extract the cells even when the module is surrounded by disturbing background and a fast method based on cumulated sums (CUSUM) change detection to extract the cell area of single-cell mini-module, where the correction of perspective distortion is implicitly done. The methods are highly automatized to allow for big data analyses. Their application to a large database of EL images substantiates that the methods work reliably on a large scale for real-world images. Simulations show that the approach achieves high accuracy, reliability and robustness. This even holds for low contrast images as evaluated by comparing the simulated accuracy for a low and a high contrast image.

On Convergence of Moments for Approximating Processes and Applications to Surrogate Models

We study critera for a pair $ (\{ X_n \} $, $ \{ Y_n \}) $ of approximating processes which guarantee closeness of moments by generalizing known results for the special case that $ Y_n = Y $ for all $n$ and $ X_n $ converges to $Y$ in probability. This problem especially arises when working with surrogate models, e.g. to enrich observed data by simulated data, where the surrogates $Y_n$'s are constructed to justify that they approximate the $ X_n $'s. The results of this paper deal with sequences of random variables. Since this framework does not cover many applications where surrogate models such as deep neural networks are used to approximate more general stochastic processes, we extend the results to the more general framework of random fields of stochastic processes. This framework especially covers image data and sequences of images. We show that uniform integrability is sufficient, and this holds even for the case of processes provided they satisfy a weak stationarity condition.

A Binary Control Chart to Detect Small Jumps

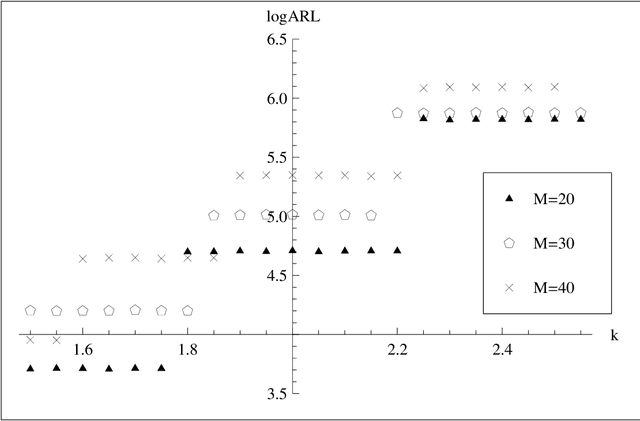
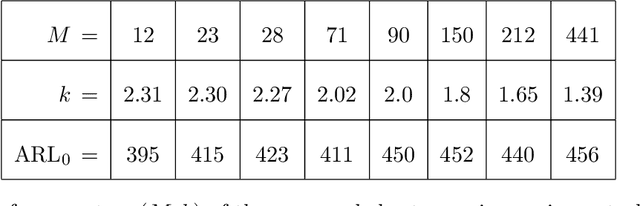
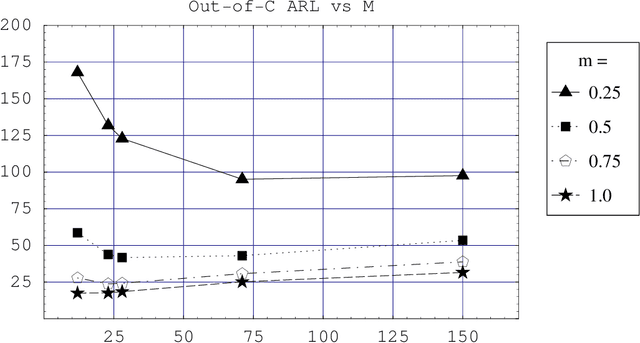
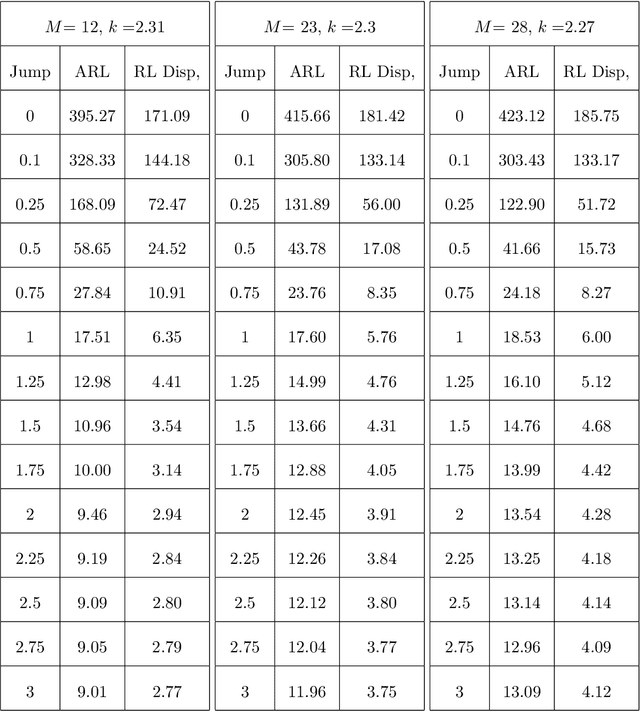
The classic N p chart gives a signal if the number of successes in a sequence of inde- pendent binary variables exceeds a control limit. Motivated by engineering applications in industrial image processing and, to some extent, financial statistics, we study a simple modification of this chart, which uses only the most recent observations. Our aim is to construct a control chart for detecting a shift of an unknown size, allowing for an unknown distribution of the error terms. Simulation studies indicate that the proposed chart is su- perior in terms of out-of-control average run length, when one is interest in the detection of very small shifts. We provide a (functional) central limit theorem under a change-point model with local alternatives which explains that unexpected and interesting behavior. Since real observations are often not independent, the question arises whether these re- sults still hold true for the dependent case. Indeed, our asymptotic results work under the fairly general condition that the observations form a martingale difference array. This enlarges the applicability of our results considerably, firstly, to a large class time series models, and, secondly, to locally dependent image data, as we demonstrate by an example.