Is there a role for statistics in artificial intelligence?

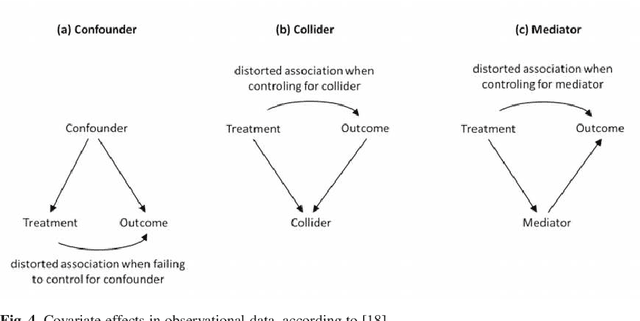
The research on and application of artificial intelligence (AI) has triggered a comprehensive scientific, economic, social and political discussion. Here we argue that statistics, as an interdisciplinary scientific field, plays a substantial role both for the theoretical and practical understanding of AI and for its future development. Statistics might even be considered a core element of AI. With its specialist knowledge of data evaluation, starting with the precise formulation of the research question and passing through a study design stage on to analysis and interpretation of the results, statistics is a natural partner for other disciplines in teaching, research and practice. This paper aims at contributing to the current discussion by highlighting the relevance of statistical methodology in the context of AI development. In particular, we discuss contributions of statistics to the field of artificial intelligence concerning methodological development, planning and design of studies, assessment of data quality and data collection, differentiation of causality and associations and assessment of uncertainty in results. Moreover, the paper also deals with the equally necessary and meaningful extension of curricula in schools and universities.

Quantitative Robustness of Localized Support Vector Machines

The huge amount of available data nowadays is a challenge for kernel-based machine learning algorithms like SVMs with respect to runtime and storage capacities. Local approaches might help to relieve these issues and to improve statistical accuracy. It has already been shown that these local approaches are consistent and robust in a basic sense. This article refines the analysis of robustness properties towards the so-called influence function which expresses the differentiability of the learning method: We show that there is a differentiable dependency of our locally learned predictor on the underlying distribution. The assumptions of the proven theorems can be verified without knowing anything about this distribution. This makes the results interesting also from an applied point of view.

Machine Learning in Official Statistics

In the first half of 2018, the Federal Statistical Office of Germany (Destatis) carried out a "Proof of Concept Machine Learning" as part of its Digital Agenda. A major component of this was surveys on the use of machine learning methods in official statistics, which were conducted at selected national and international statistical institutions and among the divisions of Destatis. It was of particular interest to find out in which statistical areas and for which tasks machine learning is used and which methods are applied. This paper is intended to make the results of the surveys publicly accessible.

Universal Consistency and Robustness of Localized Support Vector Machines

The massive amount of available data potentially used to discover patters in machine learning is a challenge for kernel based algorithms with respect to runtime and storage capacities. Local approaches might help to relieve these issues. From a statistical point of view local approaches allow additionally to deal with different structures in the data in different ways. This paper analyses properties of localized kernel based, non-parametric statistical machine learning methods, in particular of support vector machines (SVMs) and methods close to them. We will show there that locally learnt kernel methods are universal consistent. Furthermore, we give an upper bound for the maxbias in order to show statistical robustness of the proposed method.

A short note on extension theorems and their connection to universal consistency in machine learning

Statistical machine learning plays an important role in modern statistics and computer science. One main goal of statistical machine learning is to provide universally consistent algorithms, i.e., the estimator converges in probability or in some stronger sense to the Bayes risk or to the Bayes decision function. Kernel methods based on minimizing the regularized risk over a reproducing kernel Hilbert space (RKHS) belong to these statistical machine learning methods. It is in general unknown which kernel yields optimal results for a particular data set or for the unknown probability measure. Hence various kernel learning methods were proposed to choose the kernel and therefore also its RKHS in a data adaptive manner. Nevertheless, many practitioners often use the classical Gaussian RBF kernel or certain Sobolev kernels with good success. The goal of this short note is to offer one possible theoretical explanation for this empirical fact.