Post-Selection Confidence Bounds for Prediction Performance

In machine learning, the selection of a promising model from a potentially large number of competing models and the assessment of its generalization performance are critical tasks that need careful consideration. Typically, model selection and evaluation are strictly separated endeavors, splitting the sample at hand into a training, validation, and evaluation set, and only compute a single confidence interval for the prediction performance of the final selected model. We however propose an algorithm how to compute valid lower confidence bounds for multiple models that have been selected based on their prediction performances in the evaluation set by interpreting the selection problem as a simultaneous inference problem. We use bootstrap tilting and a maxT-type multiplicity correction. The approach is universally applicable for any combination of prediction models, any model selection strategy, and any prediction performance measure that accepts weights. We conducted various simulation experiments which show that our proposed approach yields lower confidence bounds that are at least comparably good as bounds from standard approaches, and that reliably reach the nominal coverage probability. In addition, especially when sample size is small, our proposed approach yields better performing prediction models than the default selection of only one model for evaluation does.

Is there a role for statistics in artificial intelligence?

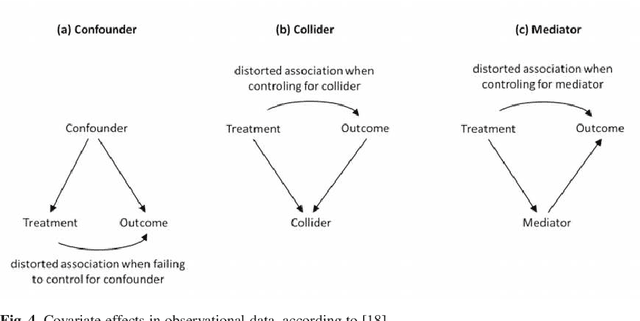
The research on and application of artificial intelligence (AI) has triggered a comprehensive scientific, economic, social and political discussion. Here we argue that statistics, as an interdisciplinary scientific field, plays a substantial role both for the theoretical and practical understanding of AI and for its future development. Statistics might even be considered a core element of AI. With its specialist knowledge of data evaluation, starting with the precise formulation of the research question and passing through a study design stage on to analysis and interpretation of the results, statistics is a natural partner for other disciplines in teaching, research and practice. This paper aims at contributing to the current discussion by highlighting the relevance of statistical methodology in the context of AI development. In particular, we discuss contributions of statistics to the field of artificial intelligence concerning methodological development, planning and design of studies, assessment of data quality and data collection, differentiation of causality and associations and assessment of uncertainty in results. Moreover, the paper also deals with the equally necessary and meaningful extension of curricula in schools and universities.

A multiple testing framework for diagnostic accuracy studies with co-primary endpoints

Major advances have been made regarding the utilization of artificial intelligence in health care. In particular, deep learning approaches have been successfully applied for automated and assisted disease diagnosis and prognosis based on complex and high-dimensional data. However, despite all justified enthusiasm, overoptimistic assessments of predictive performance are still common. Automated medical testing devices based on machine-learned prediction models should thus undergo a throughout evaluation before being implemented into clinical practice. In this work, we propose a multiple testing framework for (comparative) phase III diagnostic accuracy studies with sensitivity and specificity as co-primary endpoints. Our approach challenges the frequent recommendation to strictly separate model selection and evaluation, i.e. to only assess a single diagnostic model in the evaluation study. We show that our parametric simultaneous test procedure asymptotically allows strong control of the family-wise error rate. Moreover, we demonstrate in extensive simulation studies that our multiple testing strategy on average leads to a better final diagnostic model and increased statistical power. To plan such studies, we propose a Bayesian approach to determine the optimal number of models to evaluate. For this purpose, our algorithm optimizes the expected final model performance given previous (hold-out) data from the model development phase. We conclude that an assessment of multiple promising diagnostic models in the same evaluation study has several advantages when suitable adjustments for multiple comparisons are conducted.