Physics-informed Gaussian Processes as Linear Model Predictive Controller

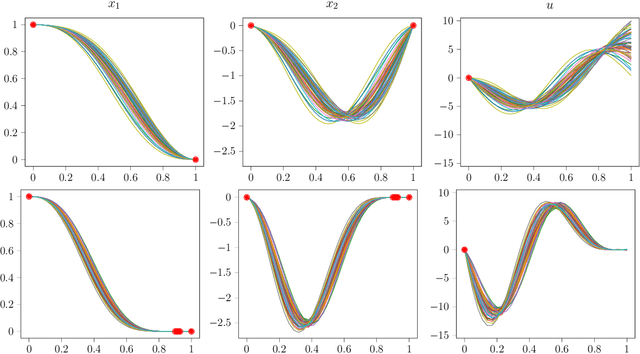
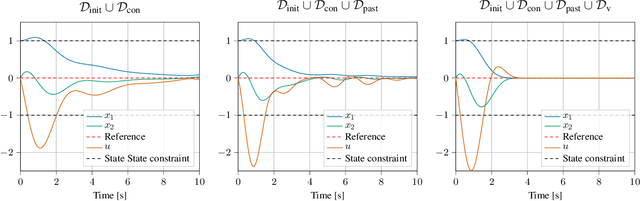
We introduce a novel algorithm for controlling linear time invariant systems in a tracking problem. The controller is based on a Gaussian Process (GP) whose realizations satisfy a system of linear ordinary differential equations with constant coefficients. Control inputs for tracking are determined by conditioning the prior GP on the setpoints, i.e. control as inference. The resulting Model Predictive Control scheme incorporates pointwise soft constraints by introducing virtual setpoints to the posterior Gaussian process. We show theoretically that our controller satisfies asymptotical stability for the optimal control problem by leveraging general results from Bayesian inference and demonstrate this result in a numerical example.

Efficiently Computable Safety Bounds for Gaussian Processes in Active Learning

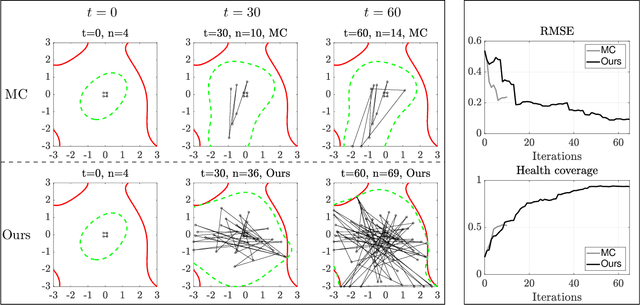
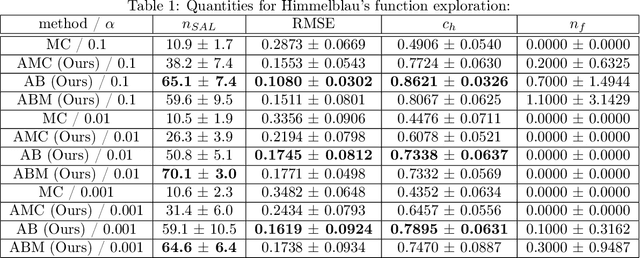
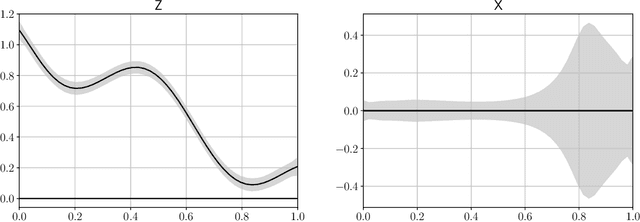
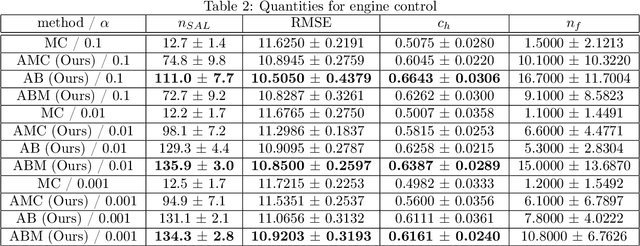
Active learning of physical systems must commonly respect practical safety constraints, which restricts the exploration of the design space. Gaussian Processes (GPs) and their calibrated uncertainty estimations are widely used for this purpose. In many technical applications the design space is explored via continuous trajectories, along which the safety needs to be assessed. This is particularly challenging for strict safety requirements in GP methods, as it employs computationally expensive Monte-Carlo sampling of high quantiles. We address these challenges by providing provable safety bounds based on the adaptively sampled median of the supremum of the posterior GP. Our method significantly reduces the number of samples required for estimating high safety probabilities, resulting in faster evaluation without sacrificing accuracy and exploration speed. The effectiveness of our safe active learning approach is demonstrated through extensive simulations and validated using a real-world engine example.