Physics-informed Gaussian Processes as Linear Model Predictive Controller

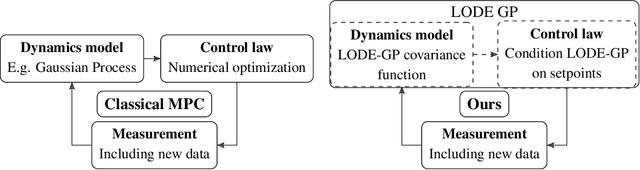
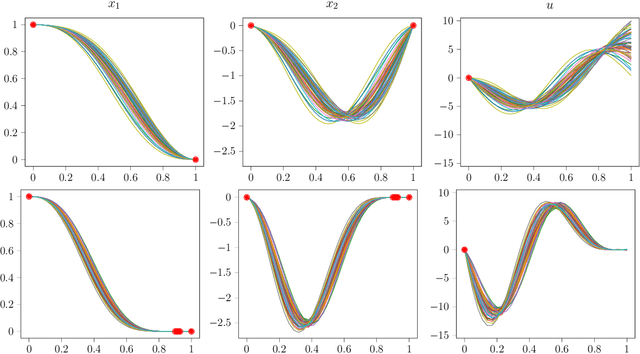
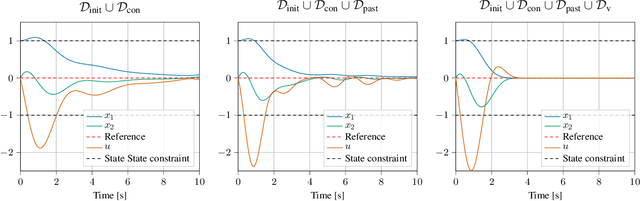
We introduce a novel algorithm for controlling linear time invariant systems in a tracking problem. The controller is based on a Gaussian Process (GP) whose realizations satisfy a system of linear ordinary differential equations with constant coefficients. Control inputs for tracking are determined by conditioning the prior GP on the setpoints, i.e. control as inference. The resulting Model Predictive Control scheme incorporates pointwise soft constraints by introducing virtual setpoints to the posterior Gaussian process. We show theoretically that our controller satisfies asymptotical stability for the optimal control problem by leveraging general results from Bayesian inference and demonstrate this result in a numerical example.

On the Laplace Approximation as Model Selection Criterion for Gaussian Processes

Model selection aims to find the best model in terms of accuracy, interpretability or simplicity, preferably all at once. In this work, we focus on evaluating model performance of Gaussian process models, i.e. finding a metric that provides the best trade-off between all those criteria. While previous work considers metrics like the likelihood, AIC or dynamic nested sampling, they either lack performance or have significant runtime issues, which severely limits applicability. We address these challenges by introducing multiple metrics based on the Laplace approximation, where we overcome a severe inconsistency occuring during naive application of the Laplace approximation. Experiments show that our metrics are comparable in quality to the gold standard dynamic nested sampling without compromising for computational speed. Our model selection criteria allow significantly faster and high quality model selection of Gaussian process models.

Constraining Gaussian Processes to Systems of Linear Ordinary Differential Equations

Data in many applications follows systems of Ordinary Differential Equations (ODEs). This paper presents a novel algorithmic and symbolic construction for covariance functions of Gaussian Processes (GPs) with realizations strictly following a system of linear homogeneous ODEs with constant coefficients, which we call LODE-GPs. Introducing this strong inductive bias into a GP improves modelling of such data. Using smith normal form algorithms, a symbolic technique, we overcome two current restrictions in the state of the art: (1) the need for certain uniqueness conditions in the set of solutions, typically assumed in classical ODE solvers and their probabilistic counterparts, and (2) the restriction to controllable systems, typically assumed when encoding differential equations in covariance functions. We show the effectiveness of LODE-GPs in a number of experiments, for example learning physically interpretable parameters by maximizing the likelihood.