Generative Models for Long Time Series: Approximately Equivariant Recurrent Network Structures for an Adjusted Training Scheme

We present a simple yet effective generative model for time series data based on a Variational Autoencoder (VAE) with recurrent layers, referred to as the Recurrent Variational Autoencoder with Subsequent Training (RVAE-ST). Our method introduces an adapted training scheme that progressively increases the sequence length, addressing the challenge recurrent layers typically face when modeling long sequences. By leveraging the recurrent architecture, the model maintains a constant number of parameters regardless of sequence length. This design encourages approximate time-shift equivariance and enables efficient modeling of long-range temporal dependencies. Rather than introducing a fundamentally new architecture, we show that a carefully composed combination of known components can match or outperform state-of-the-art generative models on several benchmark datasets. Our model performs particularly well on time series that exhibit quasi-periodic structure,while remaining competitive on datasets with more irregular or partially non-stationary behavior. We evaluate its performance using ELBO, Fr\'echet Distance, discriminative scores, and visualizations of the learned embeddings.

Gaussian Process Regression for Inverse Problems in Linear PDEs

This paper introduces a computationally efficient algorithm in system theory for solving inverse problems governed by linear partial differential equations (PDEs). We model solutions of linear PDEs using Gaussian processes with priors defined based on advanced commutative algebra and algebraic analysis. The implementation of these priors is algorithmic and achieved using the Macaulay2 computer algebra software. An example application includes identifying the wave speed from noisy data for classical wave equations, which are widely used in physics. The method achieves high accuracy while enhancing computational efficiency.

Physics-informed Gaussian Processes as Linear Model Predictive Controller

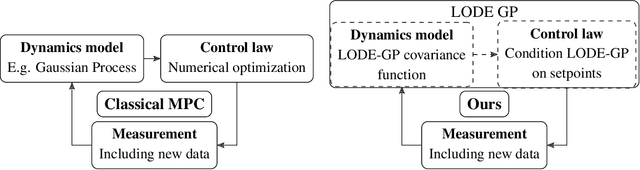
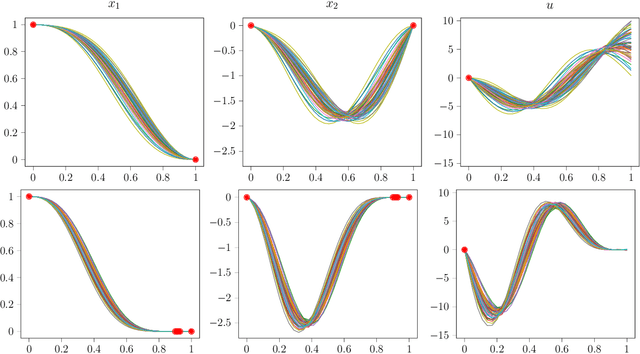
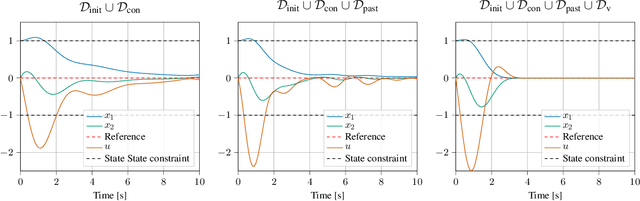
We introduce a novel algorithm for controlling linear time invariant systems in a tracking problem. The controller is based on a Gaussian Process (GP) whose realizations satisfy a system of linear ordinary differential equations with constant coefficients. Control inputs for tracking are determined by conditioning the prior GP on the setpoints, i.e. control as inference. The resulting Model Predictive Control scheme incorporates pointwise soft constraints by introducing virtual setpoints to the posterior Gaussian process. We show theoretically that our controller satisfies asymptotical stability for the optimal control problem by leveraging general results from Bayesian inference and demonstrate this result in a numerical example.

Gaussian Process Priors for Boundary Value Problems of Linear Partial Differential Equations

Solving systems of partial differential equations (PDEs) is a fundamental task in computational science, traditionally addressed by numerical solvers. Recent advancements have introduced neural operators and physics-informed neural networks (PINNs) to tackle PDEs, achieving reduced computational costs at the expense of solution quality and accuracy. Gaussian processes (GPs) have also been applied to linear PDEs, with the advantage of always yielding precise solutions. In this work, we propose Boundary Ehrenpreis-Palamodov Gaussian Processes (B-EPGPs), a novel framework for constructing GP priors that satisfy both general systems of linear PDEs with constant coefficients and linear boundary conditions. We explicitly construct GP priors for representative PDE systems with practical boundary conditions. Formal proofs of correctness are provided and empirical results demonstrating significant accuracy improvements over state-of-the-art neural operator approaches.

Visual Car Brand Classification by Implementing a Synthetic Image Dataset Creation Pipeline

Recent advancements in machine learning, particularly in deep learning and object detection, have significantly improved performance in various tasks, including image classification and synthesis. However, challenges persist, particularly in acquiring labeled data that accurately represents specific use cases. In this work, we propose an automatic pipeline for generating synthetic image datasets using Stable Diffusion, an image synthesis model capable of producing highly realistic images. We leverage YOLOv8 for automatic bounding box detection and quality assessment of synthesized images. Our contributions include demonstrating the feasibility of training image classifiers solely on synthetic data, automating the image generation pipeline, and describing the computational requirements for our approach. We evaluate the usability of different modes of Stable Diffusion and achieve a classification accuracy of 75%.

Future Aware Safe Active Learning of Time Varying Systems using Gaussian Processes

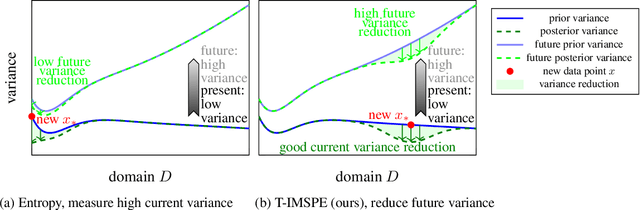
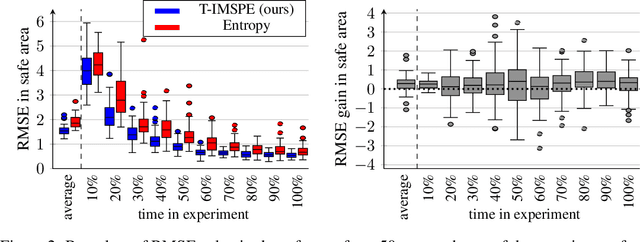
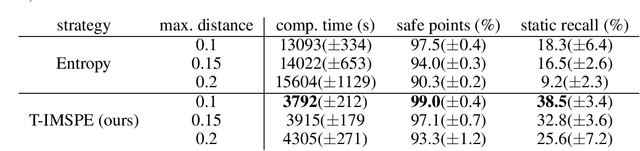
Experimental exploration of high-cost systems with safety constraints, common in engineering applications, is a challenging endeavor. Data-driven models offer a promising solution, but acquiring the requisite data remains expensive and is potentially unsafe. Safe active learning techniques prove essential, enabling the learning of high-quality models with minimal expensive data points and high safety. This paper introduces a safe active learning framework tailored for time-varying systems, addressing drift, seasonal changes, and complexities due to dynamic behavior. The proposed Time-aware Integrated Mean Squared Prediction Error (T-IMSPE) method minimizes posterior variance over current and future states, optimizing information gathering also in the time domain. Empirical results highlight T-IMSPE's advantages in model quality through toy and real-world examples. State of the art Gaussian processes are compatible with T-IMSPE. Our theoretical contributions include a clear delineation which Gaussian process kernels, domains, and weighting measures are suitable for T-IMSPE and even beyond for its non-time aware predecessor IMSPE.

PGNAA Spectral Classification of Aluminium and Copper Alloys with Machine Learning

In this paper, we explore the optimization of metal recycling with a focus on real-time differentiation between alloys of copper and aluminium. Spectral data, obtained through Prompt Gamma Neutron Activation Analysis (PGNAA), is utilized for classification. The study compares data from two detectors, cerium bromide (CeBr$_{3}$) and high purity germanium (HPGe), considering their energy resolution and sensitivity. We test various data generation, preprocessing, and classification methods, with Maximum Likelihood Classifier (MLC) and Conditional Variational Autoencoder (CVAE) yielding the best results. The study also highlights the impact of different detector types on classification accuracy, with CeBr$_{3}$ excelling in short measurement times and HPGe performing better in longer durations. The findings suggest the importance of selecting the appropriate detector and methodology based on specific application requirements.

On the Laplace Approximation as Model Selection Criterion for Gaussian Processes

Model selection aims to find the best model in terms of accuracy, interpretability or simplicity, preferably all at once. In this work, we focus on evaluating model performance of Gaussian process models, i.e. finding a metric that provides the best trade-off between all those criteria. While previous work considers metrics like the likelihood, AIC or dynamic nested sampling, they either lack performance or have significant runtime issues, which severely limits applicability. We address these challenges by introducing multiple metrics based on the Laplace approximation, where we overcome a severe inconsistency occuring during naive application of the Laplace approximation. Experiments show that our metrics are comparable in quality to the gold standard dynamic nested sampling without compromising for computational speed. Our model selection criteria allow significantly faster and high quality model selection of Gaussian process models.

Investigation of the Impact of Synthetic Training Data in the Industrial Application of Terminal Strip Object Detection

In industrial manufacturing, numerous tasks of visually inspecting or detecting specific objects exist that are currently performed manually or by classical image processing methods. Therefore, introducing recent deep learning models to industrial environments holds the potential to increase productivity and enable new applications. However, gathering and labeling sufficient data is often intractable, complicating the implementation of such projects. Hence, image synthesis methods are commonly used to generate synthetic training data from 3D models and annotate them automatically, although it results in a sim-to-real domain gap. In this paper, we investigate the sim-to-real generalization performance of standard object detectors on the complex industrial application of terminal strip object detection. Combining domain randomization and domain knowledge, we created an image synthesis pipeline for automatically generating the training data. Moreover, we manually annotated 300 real images of terminal strips for the evaluation. The results show the cruciality of the objects of interest to have the same scale in either domain. Nevertheless, under optimized scaling conditions, the sim-to-real performance difference in mean average precision amounts to 2.69 % for RetinaNet and 0.98 % for Faster R-CNN, qualifying this approach for industrial requirements.

Efficiently Computable Safety Bounds for Gaussian Processes in Active Learning

Active learning of physical systems must commonly respect practical safety constraints, which restricts the exploration of the design space. Gaussian Processes (GPs) and their calibrated uncertainty estimations are widely used for this purpose. In many technical applications the design space is explored via continuous trajectories, along which the safety needs to be assessed. This is particularly challenging for strict safety requirements in GP methods, as it employs computationally expensive Monte-Carlo sampling of high quantiles. We address these challenges by providing provable safety bounds based on the adaptively sampled median of the supremum of the posterior GP. Our method significantly reduces the number of samples required for estimating high safety probabilities, resulting in faster evaluation without sacrificing accuracy and exploration speed. The effectiveness of our safe active learning approach is demonstrated through extensive simulations and validated using a real-world engine example.