Gaussian Process Priors for Boundary Value Problems of Linear Partial Differential Equations

Solving systems of partial differential equations (PDEs) is a fundamental task in computational science, traditionally addressed by numerical solvers. Recent advancements have introduced neural operators and physics-informed neural networks (PINNs) to tackle PDEs, achieving reduced computational costs at the expense of solution quality and accuracy. Gaussian processes (GPs) have also been applied to linear PDEs, with the advantage of always yielding precise solutions. In this work, we propose Boundary Ehrenpreis-Palamodov Gaussian Processes (B-EPGPs), a novel framework for constructing GP priors that satisfy both general systems of linear PDEs with constant coefficients and linear boundary conditions. We explicitly construct GP priors for representative PDE systems with practical boundary conditions. Formal proofs of correctness are provided and empirical results demonstrating significant accuracy improvements over state-of-the-art neural operator approaches.

EEND-M2F: Masked-attention mask transformers for speaker diarization

In this paper, we make the explicit connection between image segmentation methods and end-to-end diarization methods. From these insights, we propose a novel, fully end-to-end diarization model, EEND-M2F, based on the Mask2Former architecture. Speaker representations are computed in parallel using a stack of transformer decoders, in which irrelevant frames are explicitly masked from the cross attention using predictions from previous layers. EEND-M2F is lightweight, efficient, and truly end-to-end, as it does not require any additional diarization, speaker verification, or segmentation models to run, nor does it require running any clustering algorithms. Our model achieves state-of-the-art performance on several public datasets, such as AMI, AliMeeting and RAMC. Most notably our DER of 16.07% on DIHARD-III is the first major improvement upon the challenge winning system.

Transformer Attractors for Robust and Efficient End-to-End Neural Diarization

End-to-end neural diarization with encoder-decoder based attractors (EEND-EDA) is a method to perform diarization in a single neural network. EDA handles the diarization of a flexible number of speakers by using an LSTM-based encoder-decoder that generates a set of speaker-wise attractors in an autoregressive manner. In this paper, we propose to replace EDA with a transformer-based attractor calculation (TA) module. TA is composed of a Combiner block and a Transformer decoder. The main function of the combiner block is to generate conversational dependent (CD) embeddings by incorporating learned conversational information into a global set of embeddings. These CD embeddings will then serve as the input for the transformer decoder. Results on public datasets show that EEND-TA achieves 2.68% absolute DER improvement over EEND-EDA. EEND-TA inference is 1.28 times faster than that of EEND-EDA.

Gaussian Process Priors for Systems of Linear Partial Differential Equations with Constant Coefficients

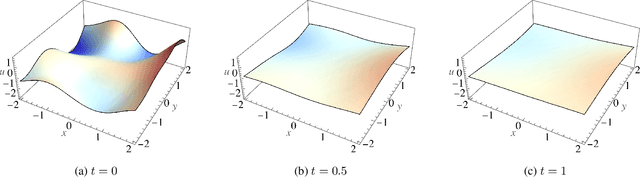
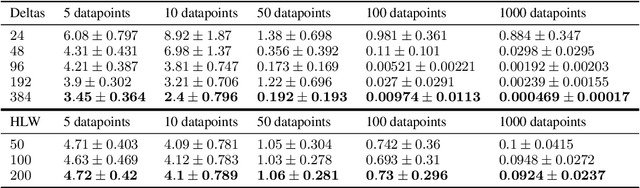
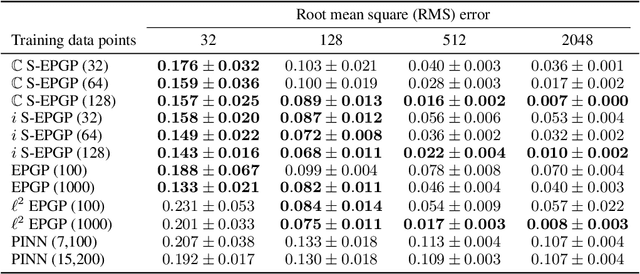
Partial differential equations (PDEs) are important tools to model physical systems, and including them into machine learning models is an important way of incorporating physical knowledge. Given any system of linear PDEs with constant coefficients, we propose a family of Gaussian process (GP) priors, which we call EPGP, such that all realizations are exact solutions of this system. We apply the Ehrenpreis-Palamodov fundamental principle, which works like a non-linear Fourier transform, to construct GP kernels mirroring standard spectral methods for GPs. Our approach can infer probable solutions of linear PDE systems from any data such as noisy measurements, or initial and boundary conditions. Constructing EPGP-priors is algorithmic, generally applicable, and comes with a sparse version (S-EPGP) that learns the relevant spectral frequencies and works better for big data sets. We demonstrate our approach on three families of systems of PDE, the heat equation, wave equation, and Maxwell's equations, where we improve upon the state of the art in computation time and precision, in some experiments by several orders of magnitude.