On the Laplace Approximation as Model Selection Criterion for Gaussian Processes

Model selection aims to find the best model in terms of accuracy, interpretability or simplicity, preferably all at once. In this work, we focus on evaluating model performance of Gaussian process models, i.e. finding a metric that provides the best trade-off between all those criteria. While previous work considers metrics like the likelihood, AIC or dynamic nested sampling, they either lack performance or have significant runtime issues, which severely limits applicability. We address these challenges by introducing multiple metrics based on the Laplace approximation, where we overcome a severe inconsistency occuring during naive application of the Laplace approximation. Experiments show that our metrics are comparable in quality to the gold standard dynamic nested sampling without compromising for computational speed. Our model selection criteria allow significantly faster and high quality model selection of Gaussian process models.

Interpreting Black-box Machine Learning Models for High Dimensional Datasets

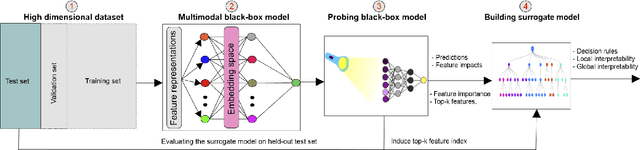
Deep neural networks (DNNs) have been shown to outperform traditional machine learning algorithms in a broad variety of application domains due to their effectiveness in modeling intricate problems and handling high-dimensional datasets. Many real-life datasets, however, are of increasingly high dimensionality, where a large number of features may be irrelevant to the task at hand. The inclusion of such features would not only introduce unwanted noise but also increase computational complexity. Furthermore, due to high non-linearity and dependency among a large number of features, DNN models tend to be unavoidably opaque and perceived as black-box methods because of their not well-understood internal functioning. A well-interpretable model can identify statistically significant features and explain the way they affect the model's outcome. In this paper, we propose an efficient method to improve the interpretability of black-box models for classification tasks in the case of high-dimensional datasets. To this end, we first train a black-box model on a high-dimensional dataset to learn the embeddings on which the classification is performed. To decompose the inner working principles of the black-box model and to identify top-k important features, we employ different probing and perturbing techniques. We then approximate the behavior of the black-box model by means of an interpretable surrogate model on the top-k feature space. Finally, we derive decision rules and local explanations from the surrogate model to explain individual decisions. Our approach outperforms and competes with state-of-the-art methods such as TabNet, XGboost, and SHAP-based interpretability techniques when tested on different datasets with varying dimensionality between 50 and 20,000.