Future Aware Safe Active Learning of Time Varying Systems using Gaussian Processes
Paper and Code
May 17, 2024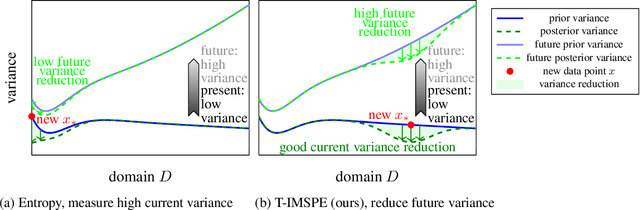

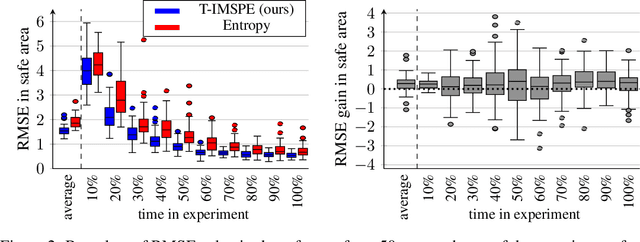
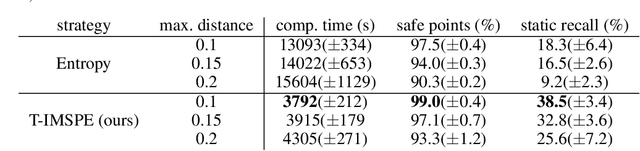
Experimental exploration of high-cost systems with safety constraints, common in engineering applications, is a challenging endeavor. Data-driven models offer a promising solution, but acquiring the requisite data remains expensive and is potentially unsafe. Safe active learning techniques prove essential, enabling the learning of high-quality models with minimal expensive data points and high safety. This paper introduces a safe active learning framework tailored for time-varying systems, addressing drift, seasonal changes, and complexities due to dynamic behavior. The proposed Time-aware Integrated Mean Squared Prediction Error (T-IMSPE) method minimizes posterior variance over current and future states, optimizing information gathering also in the time domain. Empirical results highlight T-IMSPE's advantages in model quality through toy and real-world examples. State of the art Gaussian processes are compatible with T-IMSPE. Our theoretical contributions include a clear delineation which Gaussian process kernels, domains, and weighting measures are suitable for T-IMSPE and even beyond for its non-time aware predecessor IMSPE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge