Counterfactual-based Root Cause Analysis for Dynamical Systems

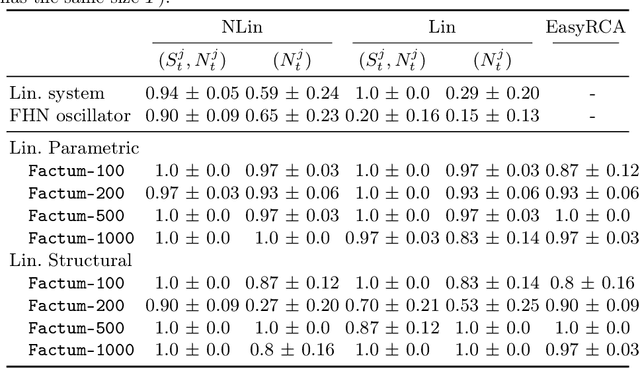
Identifying the underlying reason for a failing dynamic process or otherwise anomalous observation is a fundamental challenge, yet has numerous industrial applications. Identifying the failure-causing sub-system using causal inference, one can ask the question: "Would the observed failure also occur, if we had replaced the behaviour of a sub-system at a certain point in time with its normal behaviour?" To this end, a formal description of behaviour of the full system is needed in which such counterfactual questions can be answered. However, existing causal methods for root cause identification are typically limited to static settings and focusing on additive external influences causing failures rather than structural influences. In this paper, we address these problems by modelling the dynamic causal system using a Residual Neural Network and deriving corresponding counterfactual distributions over trajectories. We show quantitatively that more root causes are identified when an intervention is performed on the structural equation and the external influence, compared to an intervention on the external influence only. By employing an efficient approximation to a corresponding Shapley value, we also obtain a ranking between the different subsystems at different points in time being responsible for an observed failure, which is applicable in settings with large number of variables. We illustrate the effectiveness of the proposed method on a benchmark dynamic system as well as on a real world river dataset.

Estimation of Counterfactual Interventions under Uncertainties

Counterfactual analysis is intuitively performed by humans on a daily basis eg. "What should I have done differently to get the loan approved?". Such counterfactual questions also steer the formulation of scientific hypotheses. More formally it provides insights about potential improvements of a system by inferring the effects of hypothetical interventions into a past observation of the system's behaviour which plays a prominent role in a variety of industrial applications. Due to the hypothetical nature of such analysis, counterfactual distributions are inherently ambiguous. This ambiguity is particularly challenging in continuous settings in which a continuum of explanations exist for the same observation. In this paper, we address this problem by following a hierarchical Bayesian approach which explicitly models such uncertainty. In particular, we derive counterfactual distributions for a Bayesian Warped Gaussian Process thereby allowing for non-Gaussian distributions and non-additive noise. We illustrate the properties our approach on a synthetic and on a semi-synthetic example and show its performance when used within an algorithmic recourse downstream task.

Inferring the Structure of Ordinary Differential Equations

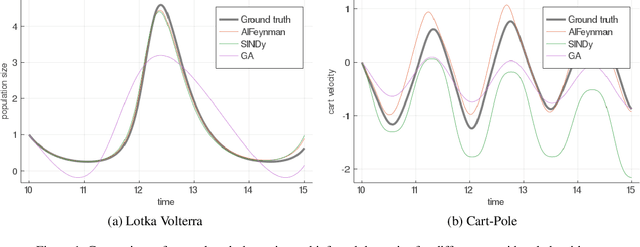
Understanding physical phenomena oftentimes means understanding the underlying dynamical system that governs observational measurements. While accurate prediction can be achieved with black box systems, they often lack interpretability and are less amenable for further expert investigation. Alternatively, the dynamics can be analysed via symbolic regression. In this paper, we extend the approach by (Udrescu et al., 2020) called AIFeynman to the dynamic setting to perform symbolic regression on ODE systems based on observations from the resulting trajectories. We compare this extension to state-of-the-art approaches for symbolic regression empirically on several dynamical systems for which the ground truth equations of increasing complexity are available. Although the proposed approach performs best on this benchmark, we observed difficulties of all the compared symbolic regression approaches on more complex systems, such as Cart-Pole.

Learning Partially Known Stochastic Dynamics with Empirical PAC Bayes

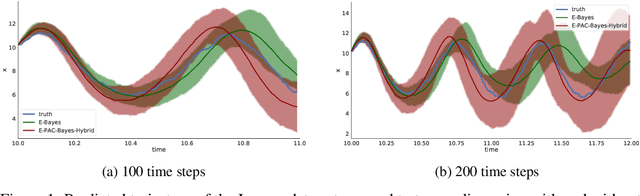
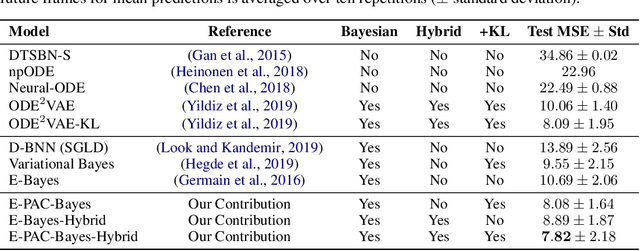
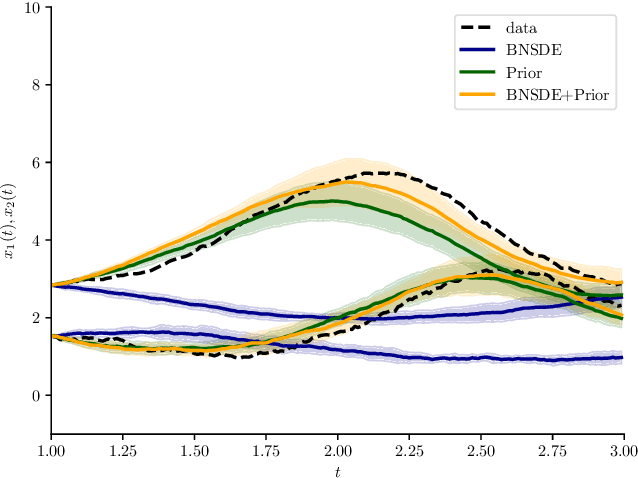
We propose a novel scheme for fitting heavily parameterized non-linear stochastic differential equations (SDEs). We assign a prior on the parameters of the SDE drift and diffusion functions to achieve a Bayesian model. We then infer this model using the well-known local reparameterized trick for the first time for empirical Bayes, i.e. to integrate out the SDE parameters. The model is then fit by maximizing the likelihood of the resultant marginal with respect to a potentially large number of hyperparameters, which prohibits stable training. As the prior parameters are marginalized, the model also no longer provides a principled means to incorporate prior knowledge. We overcome both of these drawbacks by deriving a training loss that comprises the marginal likelihood of the predictor and a PAC-Bayesian complexity penalty. We observe on synthetic as well as real-world time series prediction tasks that our method provides an improved model fit accompanied with favorable extrapolation properties when provided a partial description of the environment dynamics. Hence, we view the outcome as a promising attempt for building cutting-edge hybrid learning systems that effectively combine first-principle physics and data-driven approaches.

Bayesian Prior Networks with PAC Training

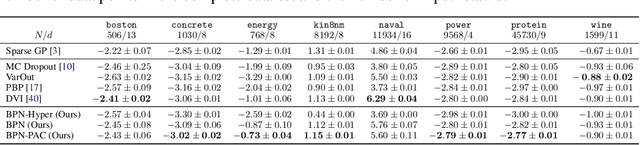
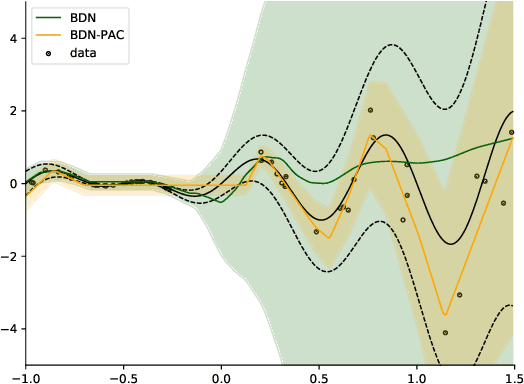
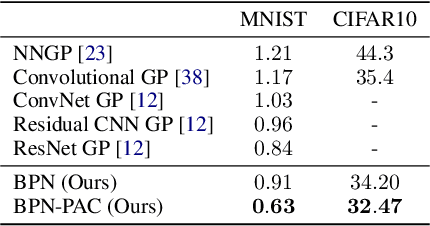
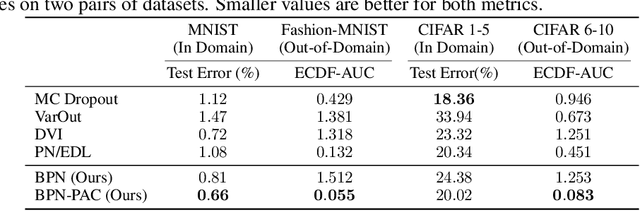
We propose to train Bayesian Neural Networks (BNNs) by empirical Bayes as an alternative to posterior weight inference. By approximately marginalizing out an i.i.d.\ realization of a finite number of sibling weights per data-point using the Central Limit Theorem (CLT), we attain a scalable and effective Bayesian deep predictor. This approach directly models the posterior predictive distribution, by-passing the intractable posterior weight inference step. However, it introduces a prohibitively large number of hyperparameters for stable training. As the prior weights are marginalized and hyperparameters are optimized, the model also no longer provides a means to incorporate prior knowledge. We overcome both of these drawbacks by deriving a trivial PAC bound that comprises the marginal likelihood of the predictor and a complexity penalty. The outcome integrates organically into the prior networks framework, bringing about an effective and holistic Bayesian treatment of prediction uncertainty. We observe on various regression, classification, and out-of-domain detection benchmarks that our scalable method provides an improved model fit accompanied with significantly better uncertainty estimates than the state-of-the-art.

Learning Gaussian Processes by Minimizing PAC-Bayesian Generalization Bounds

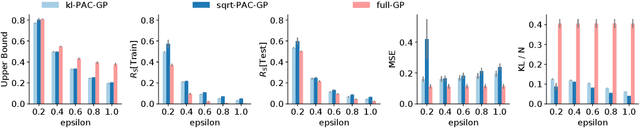
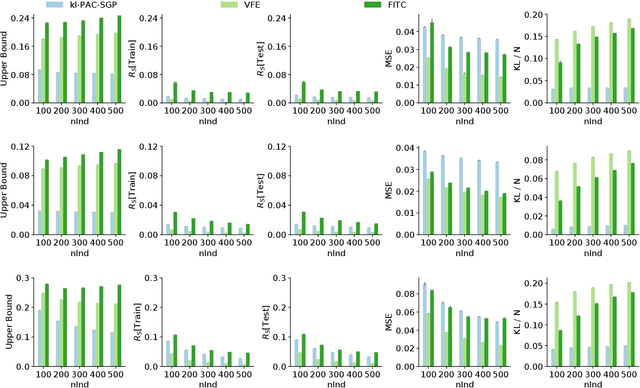
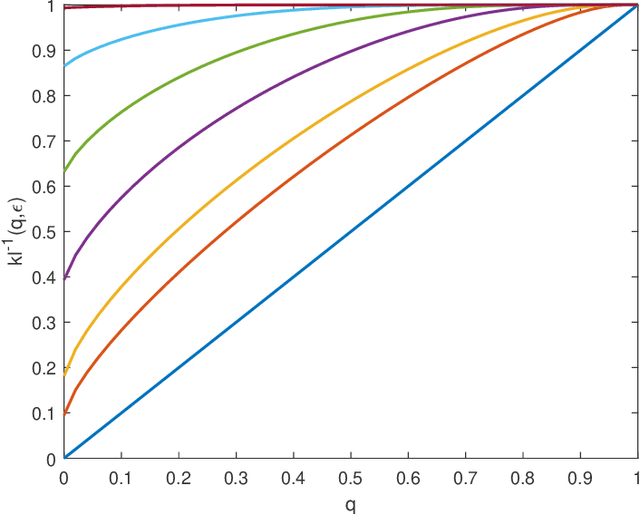
Gaussian Processes (GPs) are a generic modelling tool for supervised learning. While they have been successfully applied on large datasets, their use in safety-critical applications is hindered by the lack of good performance guarantees. To this end, we propose a method to learn GPs and their sparse approximations by directly optimizing a PAC-Bayesian bound on their generalization performance, instead of maximizing the marginal likelihood. Besides its theoretical appeal, we find in our evaluation that our learning method is robust and yields significantly better generalization guarantees than other common GP approaches on several regression benchmark datasets.

In All Likelihood, Deep Belief Is Not Enough

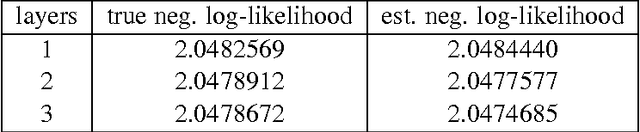
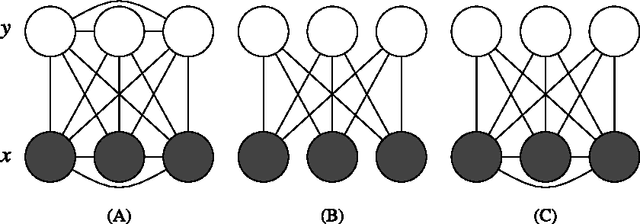
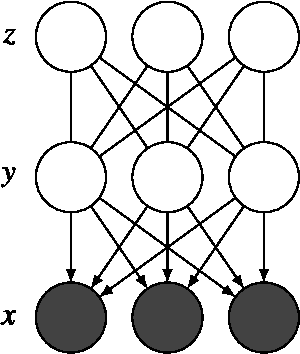
Statistical models of natural stimuli provide an important tool for researchers in the fields of machine learning and computational neuroscience. A canonical way to quantitatively assess and compare the performance of statistical models is given by the likelihood. One class of statistical models which has recently gained increasing popularity and has been applied to a variety of complex data are deep belief networks. Analyses of these models, however, have been typically limited to qualitative analyses based on samples due to the computationally intractable nature of the model likelihood. Motivated by these circumstances, the present article provides a consistent estimator for the likelihood that is both computationally tractable and simple to apply in practice. Using this estimator, a deep belief network which has been suggested for the modeling of natural image patches is quantitatively investigated and compared to other models of natural image patches. Contrary to earlier claims based on qualitative results, the results presented in this article provide evidence that the model under investigation is not a particularly good model for natural images