Counterfactual-based Root Cause Analysis for Dynamical Systems
Paper and Code
Jun 12, 2024

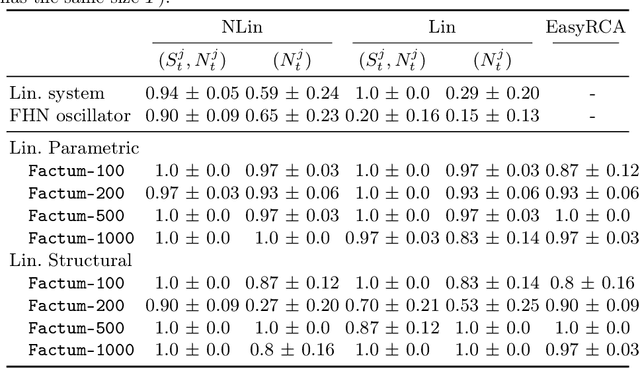

Identifying the underlying reason for a failing dynamic process or otherwise anomalous observation is a fundamental challenge, yet has numerous industrial applications. Identifying the failure-causing sub-system using causal inference, one can ask the question: "Would the observed failure also occur, if we had replaced the behaviour of a sub-system at a certain point in time with its normal behaviour?" To this end, a formal description of behaviour of the full system is needed in which such counterfactual questions can be answered. However, existing causal methods for root cause identification are typically limited to static settings and focusing on additive external influences causing failures rather than structural influences. In this paper, we address these problems by modelling the dynamic causal system using a Residual Neural Network and deriving corresponding counterfactual distributions over trajectories. We show quantitatively that more root causes are identified when an intervention is performed on the structural equation and the external influence, compared to an intervention on the external influence only. By employing an efficient approximation to a corresponding Shapley value, we also obtain a ranking between the different subsystems at different points in time being responsible for an observed failure, which is applicable in settings with large number of variables. We illustrate the effectiveness of the proposed method on a benchmark dynamic system as well as on a real world river dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge