Juliane Weilbach
Counterfactual-based Root Cause Analysis for Dynamical Systems
Jun 12, 2024

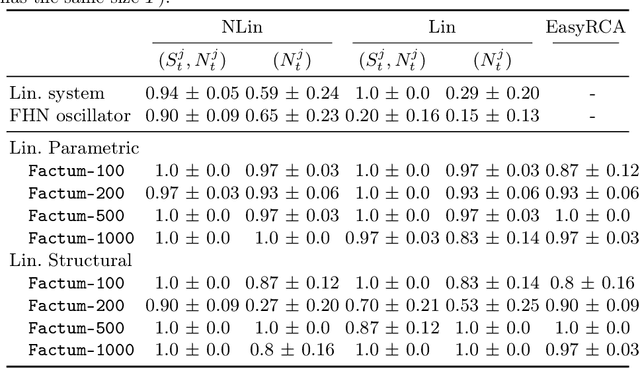

Abstract:Identifying the underlying reason for a failing dynamic process or otherwise anomalous observation is a fundamental challenge, yet has numerous industrial applications. Identifying the failure-causing sub-system using causal inference, one can ask the question: "Would the observed failure also occur, if we had replaced the behaviour of a sub-system at a certain point in time with its normal behaviour?" To this end, a formal description of behaviour of the full system is needed in which such counterfactual questions can be answered. However, existing causal methods for root cause identification are typically limited to static settings and focusing on additive external influences causing failures rather than structural influences. In this paper, we address these problems by modelling the dynamic causal system using a Residual Neural Network and deriving corresponding counterfactual distributions over trajectories. We show quantitatively that more root causes are identified when an intervention is performed on the structural equation and the external influence, compared to an intervention on the external influence only. By employing an efficient approximation to a corresponding Shapley value, we also obtain a ranking between the different subsystems at different points in time being responsible for an observed failure, which is applicable in settings with large number of variables. We illustrate the effectiveness of the proposed method on a benchmark dynamic system as well as on a real world river dataset.
Estimation of Counterfactual Interventions under Uncertainties
Sep 15, 2023Abstract:Counterfactual analysis is intuitively performed by humans on a daily basis eg. "What should I have done differently to get the loan approved?". Such counterfactual questions also steer the formulation of scientific hypotheses. More formally it provides insights about potential improvements of a system by inferring the effects of hypothetical interventions into a past observation of the system's behaviour which plays a prominent role in a variety of industrial applications. Due to the hypothetical nature of such analysis, counterfactual distributions are inherently ambiguous. This ambiguity is particularly challenging in continuous settings in which a continuum of explanations exist for the same observation. In this paper, we address this problem by following a hierarchical Bayesian approach which explicitly models such uncertainty. In particular, we derive counterfactual distributions for a Bayesian Warped Gaussian Process thereby allowing for non-Gaussian distributions and non-additive noise. We illustrate the properties our approach on a synthetic and on a semi-synthetic example and show its performance when used within an algorithmic recourse downstream task.
Inferring the Structure of Ordinary Differential Equations
Jul 05, 2021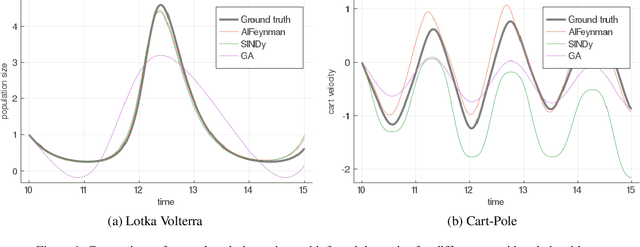



Abstract:Understanding physical phenomena oftentimes means understanding the underlying dynamical system that governs observational measurements. While accurate prediction can be achieved with black box systems, they often lack interpretability and are less amenable for further expert investigation. Alternatively, the dynamics can be analysed via symbolic regression. In this paper, we extend the approach by (Udrescu et al., 2020) called AIFeynman to the dynamic setting to perform symbolic regression on ODE systems based on observations from the resulting trajectories. We compare this extension to state-of-the-art approaches for symbolic regression empirically on several dynamical systems for which the ground truth equations of increasing complexity are available. Although the proposed approach performs best on this benchmark, we observed difficulties of all the compared symbolic regression approaches on more complex systems, such as Cart-Pole.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge