Bayesian Prior Networks with PAC Training

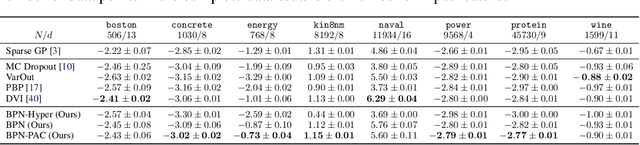
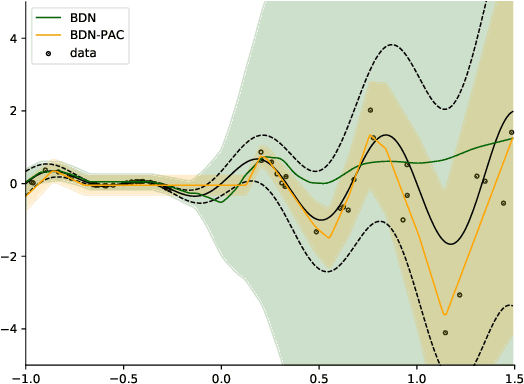
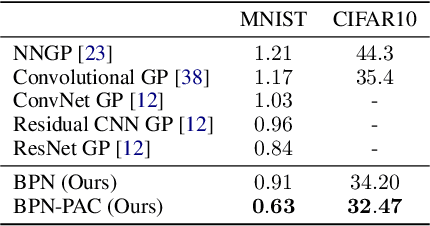
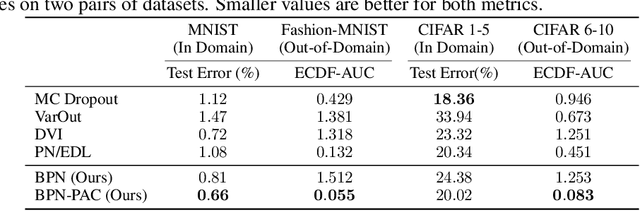
We propose to train Bayesian Neural Networks (BNNs) by empirical Bayes as an alternative to posterior weight inference. By approximately marginalizing out an i.i.d.\ realization of a finite number of sibling weights per data-point using the Central Limit Theorem (CLT), we attain a scalable and effective Bayesian deep predictor. This approach directly models the posterior predictive distribution, by-passing the intractable posterior weight inference step. However, it introduces a prohibitively large number of hyperparameters for stable training. As the prior weights are marginalized and hyperparameters are optimized, the model also no longer provides a means to incorporate prior knowledge. We overcome both of these drawbacks by deriving a trivial PAC bound that comprises the marginal likelihood of the predictor and a complexity penalty. The outcome integrates organically into the prior networks framework, bringing about an effective and holistic Bayesian treatment of prediction uncertainty. We observe on various regression, classification, and out-of-domain detection benchmarks that our scalable method provides an improved model fit accompanied with significantly better uncertainty estimates than the state-of-the-art.