Entropy-Based Uncertainty Modeling for Trajectory Prediction in Autonomous Driving

In autonomous driving, accurate motion prediction is essential for safe and efficient motion planning. To ensure safety, planners must rely on reliable uncertainty information about the predicted future behavior of surrounding agents, yet this aspect has received limited attention. This paper addresses the so-far neglected problem of uncertainty modeling in trajectory prediction. We adopt a holistic approach that focuses on uncertainty quantification, decomposition, and the influence of model composition. Our method is based on a theoretically grounded information-theoretic approach to measure uncertainty, allowing us to decompose total uncertainty into its aleatoric and epistemic components. We conduct extensive experiments on the nuScenes dataset to assess how different model architectures and configurations affect uncertainty quantification and model robustness.

Motion Forecasting via Model-Based Risk Minimization

Forecasting the future trajectories of surrounding agents is crucial for autonomous vehicles to ensure safe, efficient, and comfortable route planning. While model ensembling has improved prediction accuracy in various fields, its application in trajectory prediction is limited due to the multi-modal nature of predictions. In this paper, we propose a novel sampling method applicable to trajectory prediction based on the predictions of multiple models. We first show that conventional sampling based on predicted probabilities can degrade performance due to missing alignment between models. To address this problem, we introduce a new method that generates optimal trajectories from a set of neural networks, framing it as a risk minimization problem with a variable loss function. By using state-of-the-art models as base learners, our approach constructs diverse and effective ensembles for optimal trajectory sampling. Extensive experiments on the nuScenes prediction dataset demonstrate that our method surpasses current state-of-the-art techniques, achieving top ranks on the leaderboard. We also provide a comprehensive empirical study on ensembling strategies, offering insights into their effectiveness. Our findings highlight the potential of advanced ensembling techniques in trajectory prediction, significantly improving predictive performance and paving the way for more reliable predicted trajectories.

Sampling-Free Probabilistic Deep State-Space Models

Many real-world dynamical systems can be described as State-Space Models (SSMs). In this formulation, each observation is emitted by a latent state, which follows first-order Markovian dynamics. A Probabilistic Deep SSM (ProDSSM) generalizes this framework to dynamical systems of unknown parametric form, where the transition and emission models are described by neural networks with uncertain weights. In this work, we propose the first deterministic inference algorithm for models of this type. Our framework allows efficient approximations for training and testing. We demonstrate in our experiments that our new method can be employed for a variety of tasks and enjoys a superior balance between predictive performance and computational budget.

Can you text what is happening? Integrating pre-trained language encoders into trajectory prediction models for autonomous driving

In autonomous driving tasks, scene understanding is the first step towards predicting the future behavior of the surrounding traffic participants. Yet, how to represent a given scene and extract its features are still open research questions. In this study, we propose a novel text-based representation of traffic scenes and process it with a pre-trained language encoder. First, we show that text-based representations, combined with classical rasterized image representations, lead to descriptive scene embeddings. Second, we benchmark our predictions on the nuScenes dataset and show significant improvements compared to baselines. Third, we show in an ablation study that a joint encoder of text and rasterized images outperforms the individual encoders confirming that both representations have their complementary strengths.

Cheap and Deterministic Inference for Deep State-Space Models of Interacting Dynamical Systems

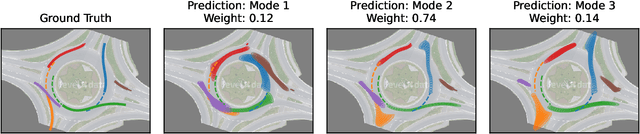
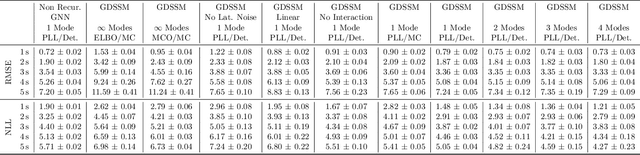
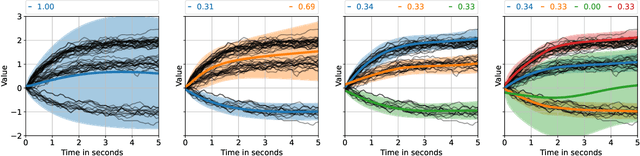
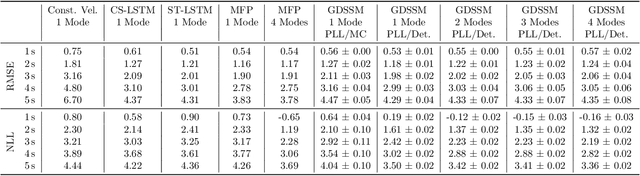
Graph neural networks are often used to model interacting dynamical systems since they gracefully scale to systems with a varying and high number of agents. While there has been much progress made for deterministic interacting systems, modeling is much more challenging for stochastic systems in which one is interested in obtaining a predictive distribution over future trajectories. Existing methods are either computationally slow since they rely on Monte Carlo sampling or make simplifying assumptions such that the predictive distribution is unimodal. In this work, we present a deep state-space model which employs graph neural networks in order to model the underlying interacting dynamical system. The predictive distribution is multimodal and has the form of a Gaussian mixture model, where the moments of the Gaussian components can be computed via deterministic moment matching rules. Our moment matching scheme can be exploited for sample-free inference, leading to more efficient and stable training compared to Monte Carlo alternatives. Furthermore, we propose structured approximations to the covariance matrices of the Gaussian components in order to scale up to systems with many agents. We benchmark our novel framework on two challenging autonomous driving datasets. Both confirm the benefits of our method compared to state-of-the-art methods. We further demonstrate the usefulness of our individual contributions in a carefully designed ablation study and provide a detailed runtime analysis of our proposed covariance approximations. Finally, we empirically demonstrate the generalization ability of our method by evaluating its performance on unseen scenarios.

Differentiable Implicit Layers

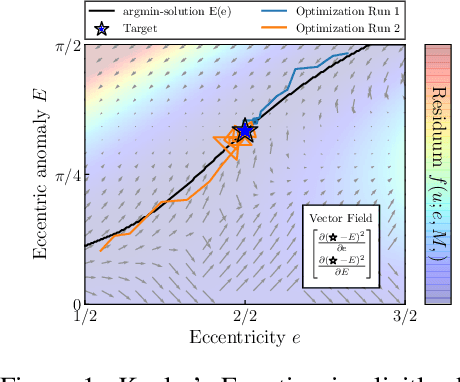
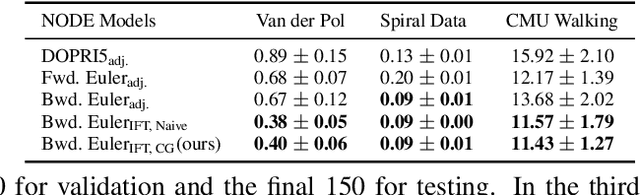
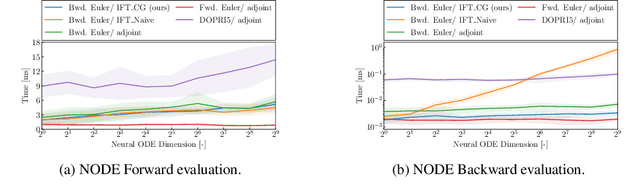
In this paper, we introduce an efficient backpropagation scheme for non-constrained implicit functions. These functions are parametrized by a set of learnable weights and may optionally depend on some input; making them perfectly suitable as learnable layer in a neural network. We demonstrate our scheme on different applications: (i) neural ODEs with the implicit Euler method, and (ii) system identification in model predictive control.

Learning Partially Known Stochastic Dynamics with Empirical PAC Bayes

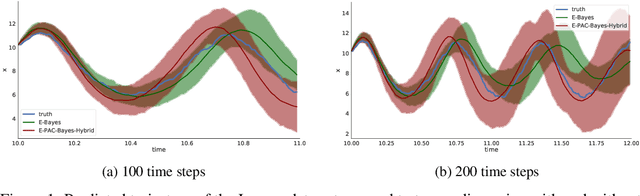
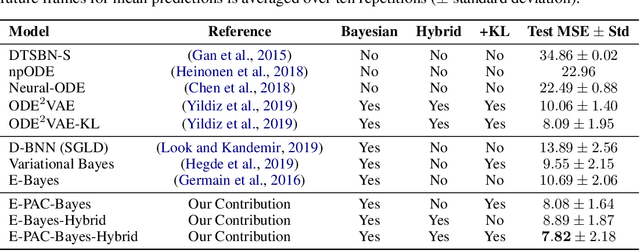
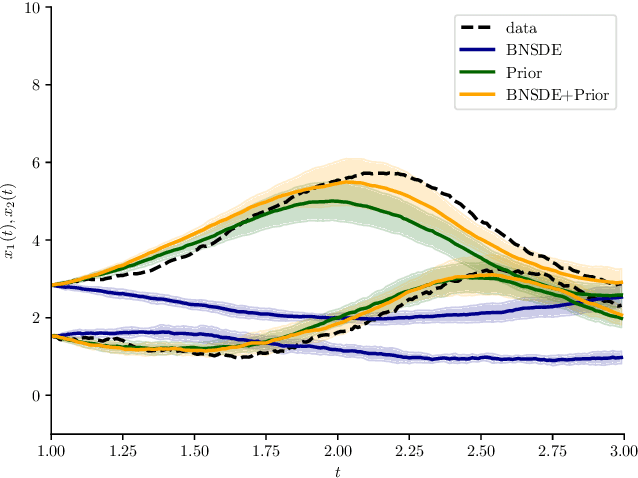
We propose a novel scheme for fitting heavily parameterized non-linear stochastic differential equations (SDEs). We assign a prior on the parameters of the SDE drift and diffusion functions to achieve a Bayesian model. We then infer this model using the well-known local reparameterized trick for the first time for empirical Bayes, i.e. to integrate out the SDE parameters. The model is then fit by maximizing the likelihood of the resultant marginal with respect to a potentially large number of hyperparameters, which prohibits stable training. As the prior parameters are marginalized, the model also no longer provides a principled means to incorporate prior knowledge. We overcome both of these drawbacks by deriving a training loss that comprises the marginal likelihood of the predictor and a PAC-Bayesian complexity penalty. We observe on synthetic as well as real-world time series prediction tasks that our method provides an improved model fit accompanied with favorable extrapolation properties when provided a partial description of the environment dynamics. Hence, we view the outcome as a promising attempt for building cutting-edge hybrid learning systems that effectively combine first-principle physics and data-driven approaches.

Deterministic Inference of Neural Stochastic Differential Equations

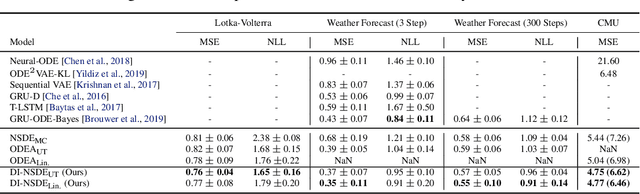
Model noise is known to have detrimental effects on neural networks, such as training instability and predictive distributions with non-calibrated uncertainty properties. These factors set bottlenecks on the expressive potential of Neural Stochastic Differential Equations (NSDEs), a model family that employs neural nets on both drift and diffusion functions. We introduce a novel algorithm that solves a generic NSDE using only deterministic approximation methods. Given a discretization, we estimate the marginal distribution of the It\^{o} process implied by the NSDE using a recursive scheme to propagate deterministic approximations of the statistical moments across time steps. The proposed algorithm comes with theoretical guarantees on numerical stability and convergence to the true solution, enabling its computational use for robust, accurate, and efficient prediction of long sequences. We observe our novel algorithm to behave interpretably on synthetic setups and to improve the state of the art on two challenging real-world tasks.