Cheap and Deterministic Inference for Deep State-Space Models of Interacting Dynamical Systems
Paper and Code
May 02, 2023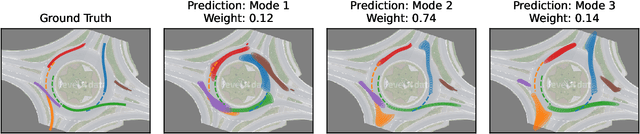
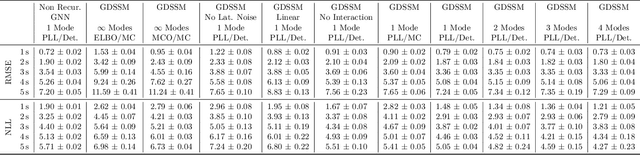
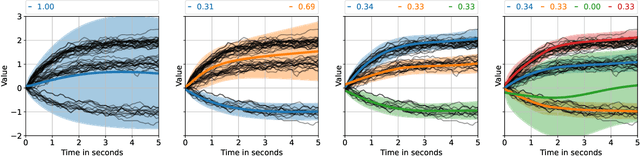
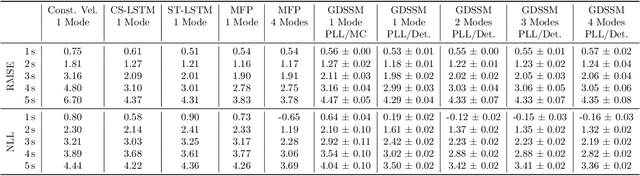
Graph neural networks are often used to model interacting dynamical systems since they gracefully scale to systems with a varying and high number of agents. While there has been much progress made for deterministic interacting systems, modeling is much more challenging for stochastic systems in which one is interested in obtaining a predictive distribution over future trajectories. Existing methods are either computationally slow since they rely on Monte Carlo sampling or make simplifying assumptions such that the predictive distribution is unimodal. In this work, we present a deep state-space model which employs graph neural networks in order to model the underlying interacting dynamical system. The predictive distribution is multimodal and has the form of a Gaussian mixture model, where the moments of the Gaussian components can be computed via deterministic moment matching rules. Our moment matching scheme can be exploited for sample-free inference, leading to more efficient and stable training compared to Monte Carlo alternatives. Furthermore, we propose structured approximations to the covariance matrices of the Gaussian components in order to scale up to systems with many agents. We benchmark our novel framework on two challenging autonomous driving datasets. Both confirm the benefits of our method compared to state-of-the-art methods. We further demonstrate the usefulness of our individual contributions in a carefully designed ablation study and provide a detailed runtime analysis of our proposed covariance approximations. Finally, we empirically demonstrate the generalization ability of our method by evaluating its performance on unseen scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge