Deterministic Inference of Neural Stochastic Differential Equations

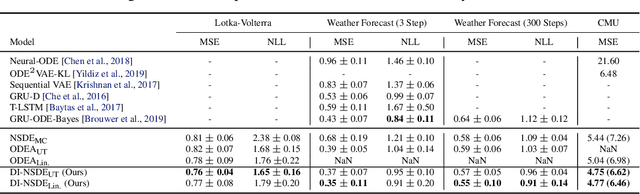
Model noise is known to have detrimental effects on neural networks, such as training instability and predictive distributions with non-calibrated uncertainty properties. These factors set bottlenecks on the expressive potential of Neural Stochastic Differential Equations (NSDEs), a model family that employs neural nets on both drift and diffusion functions. We introduce a novel algorithm that solves a generic NSDE using only deterministic approximation methods. Given a discretization, we estimate the marginal distribution of the It\^{o} process implied by the NSDE using a recursive scheme to propagate deterministic approximations of the statistical moments across time steps. The proposed algorithm comes with theoretical guarantees on numerical stability and convergence to the true solution, enabling its computational use for robust, accurate, and efficient prediction of long sequences. We observe our novel algorithm to behave interpretably on synthetic setups and to improve the state of the art on two challenging real-world tasks.