Diffusion Schrödinger Bridge Matching
Paper and Code
Mar 29, 2023
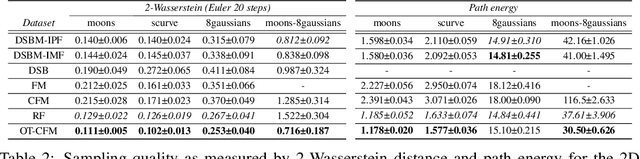

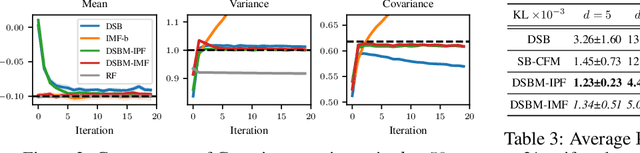
Solving transport problems, i.e. finding a map transporting one given distribution to another, has numerous applications in machine learning. Novel mass transport methods motivated by generative modeling have recently been proposed, e.g. Denoising Diffusion Models (DDMs) and Flow Matching Models (FMMs) implement such a transport through a Stochastic Differential Equation (SDE) or an Ordinary Differential Equation (ODE). However, while it is desirable in many applications to approximate the deterministic dynamic Optimal Transport (OT) map which admits attractive properties, DDMs and FMMs are not guaranteed to provide transports close to the OT map. In contrast, Schr\"odinger bridges (SBs) compute stochastic dynamic mappings which recover entropy-regularized versions of OT. Unfortunately, existing numerical methods approximating SBs either scale poorly with dimension or accumulate errors across iterations. In this work, we introduce Iterative Markovian Fitting, a new methodology for solving SB problems, and Diffusion Schr\"odinger Bridge Matching (DSBM), a novel numerical algorithm for computing IMF iterates. DSBM significantly improves over previous SB numerics and recovers as special/limiting cases various recent transport methods. We demonstrate the performance of DSBM on a variety of problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge