EASE-TTT: Evidence-Aligned Selective Test-Time Training for Long-Context Question Answering

Long-context question answering (QA) remains challenging for smaller language models even when answer-bearing evidence is already present in the input. Existing within-context retrieval methods localize and expose candidate evidence chunks for the question, but they stop at input-level evidence exposure rather than adapting the query-side attention parameters that control how the model allocates attention over full-context positions. In contrast, lightweight test-time adaptation methods, such as query-only test-time training (qTTT), leave evidence localization unresolved because their generic span-level self-supervised objectives do not identify which context positions support the current answer. In this paper, we propose Evidence-Aligned SElective Test-Time Training (EASE-TTT), a within-context retrieval-augmented test-time training framework that converts selected evidence chunks into a soft attention supervision target over their token positions. Instead of replacing the full context with retrieved chunks, EASE-TTT uses the resulting attention target to guide query-side adaptation, with the adapted model generating the final answer from the original full context. Experiments on six LongBench QA tasks and three small decoder-only language models show that EASE-TTT achieves the strongest macro-average performance among full-context inference, retrieval-only baselines, and qTTT, supporting evidence-aligned test-time adaptation in long-context QA.

Ranking of Large Language Model with Nonparametric Prompts

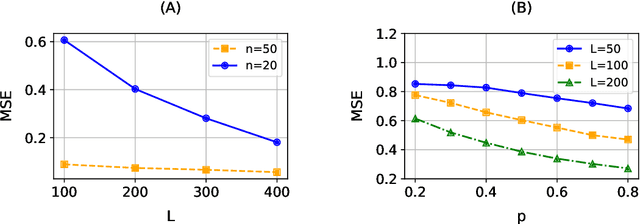
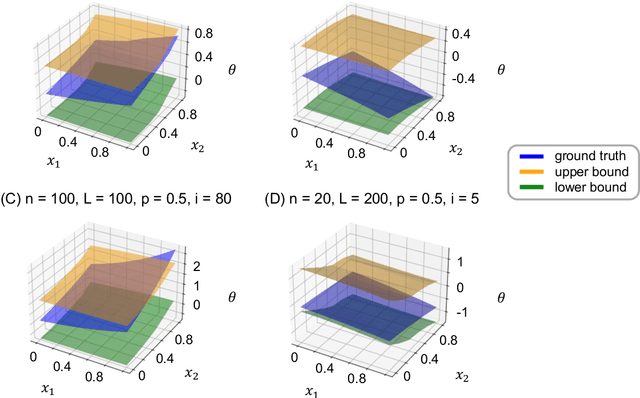
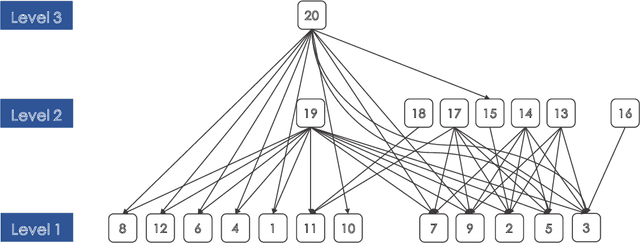
We consider the inference for the ranking of large language models (LLMs). Alignment arises as a big challenge to mitigate hallucinations in the use of LLMs. Ranking LLMs has been shown as a well-performing tool to improve alignment based on the best-of-$N$ policy. In this paper, we propose a new inferential framework for testing hypotheses and constructing confidence intervals of the ranking of language models. We consider the widely adopted Bradley-Terry-Luce (BTL) model, where each item is assigned a positive preference score that determines its pairwise comparisons' outcomes. We further extend it into the contextual setting, where the score of each model varies with the prompt. We show the convergence rate of our estimator. By extending the current Gaussian multiplier bootstrap theory to accommodate the supremum of not identically distributed empirical processes, we construct the confidence interval for ranking and propose a valid testing procedure. We also introduce the confidence diagram as a global ranking property. We conduct numerical experiments to assess the performance of our method.