Inference of Dependency Knowledge Graph for Electronic Health Records

The effective analysis of high-dimensional Electronic Health Record (EHR) data, with substantial potential for healthcare research, presents notable methodological challenges. Employing predictive modeling guided by a knowledge graph (KG), which enables efficient feature selection, can enhance both statistical efficiency and interpretability. While various methods have emerged for constructing KGs, existing techniques often lack statistical certainty concerning the presence of links between entities, especially in scenarios where the utilization of patient-level EHR data is limited due to privacy concerns. In this paper, we propose the first inferential framework for deriving a sparse KG with statistical guarantee based on the dynamic log-linear topic model proposed by \cite{arora2016latent}. Within this model, the KG embeddings are estimated by performing singular value decomposition on the empirical pointwise mutual information matrix, offering a scalable solution. We then establish entrywise asymptotic normality for the KG low-rank estimator, enabling the recovery of sparse graph edges with controlled type I error. Our work uniquely addresses the under-explored domain of statistical inference about non-linear statistics under the low-rank temporal dependent models, a critical gap in existing research. We validate our approach through extensive simulation studies and then apply the method to real-world EHR data in constructing clinical KGs and generating clinical feature embeddings.

Combinatorial Inference on the Optimal Assortment in Multinomial Logit Models

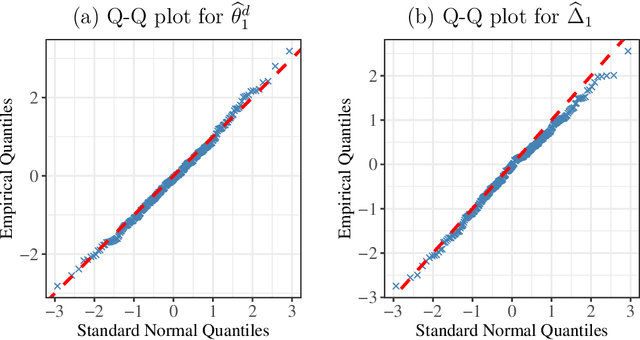
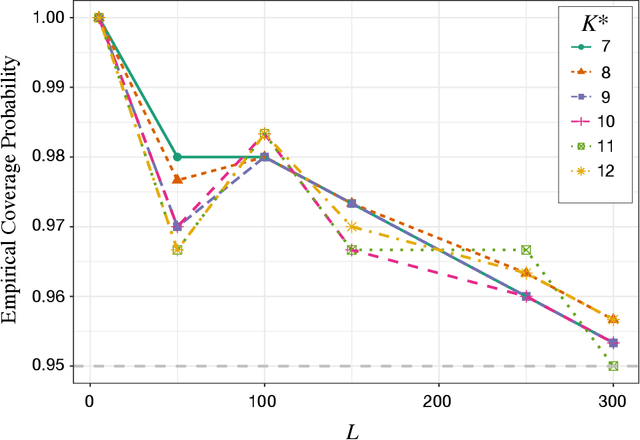
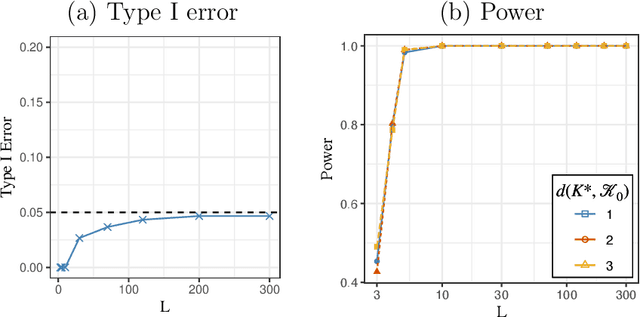
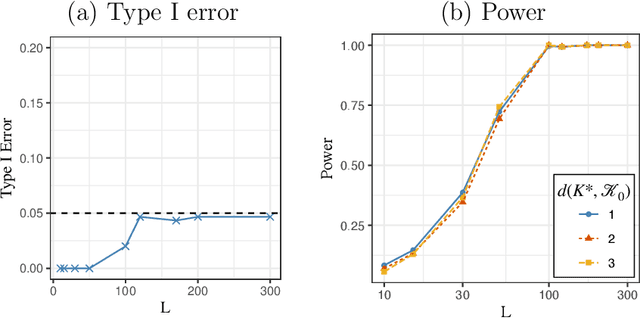
Assortment optimization has received active explorations in the past few decades due to its practical importance. Despite the extensive literature dealing with optimization algorithms and latent score estimation, uncertainty quantification for the optimal assortment still needs to be explored and is of great practical significance. Instead of estimating and recovering the complete optimal offer set, decision-makers may only be interested in testing whether a given property holds true for the optimal assortment, such as whether they should include several products of interest in the optimal set, or how many categories of products the optimal set should include. This paper proposes a novel inferential framework for testing such properties. We consider the widely adopted multinomial logit (MNL) model, where we assume that each customer will purchase an item within the offered products with a probability proportional to the underlying preference score associated with the product. We reduce inferring a general optimal assortment property to quantifying the uncertainty associated with the sign change point detection of the marginal revenue gaps. We show the asymptotic normality of the marginal revenue gap estimator, and construct a maximum statistic via the gap estimators to detect the sign change point. By approximating the distribution of the maximum statistic with multiplier bootstrap techniques, we propose a valid testing procedure. We also conduct numerical experiments to assess the performance of our method.