Numerical Methods for Convex Multistage Stochastic Optimization

Optimization problems involving sequential decisions in a stochastic environment were studied in Stochastic Programming (SP), Stochastic Optimal Control (SOC) and Markov Decision Processes (MDP). In this paper we mainly concentrate on SP and SOC modelling approaches. In these frameworks there are natural situations when the considered problems are convex. Classical approach to sequential optimization is based on dynamic programming. It has the problem of the so-called ``Curse of Dimensionality", in that its computational complexity increases exponentially with increase of dimension of state variables. Recent progress in solving convex multistage stochastic problems is based on cutting planes approximations of the cost-to-go (value) functions of dynamic programming equations. Cutting planes type algorithms in dynamical settings is one of the main topics of this paper. We also discuss Stochastic Approximation type methods applied to multistage stochastic optimization problems. From the computational complexity point of view, these two types of methods seem to be complimentary to each other. Cutting plane type methods can handle multistage problems with a large number of stages, but a relatively smaller number of state (decision) variables. On the other hand, stochastic approximation type methods can only deal with a small number of stages, but a large number of decision variables.

Goodness-of-fit tests on manifolds

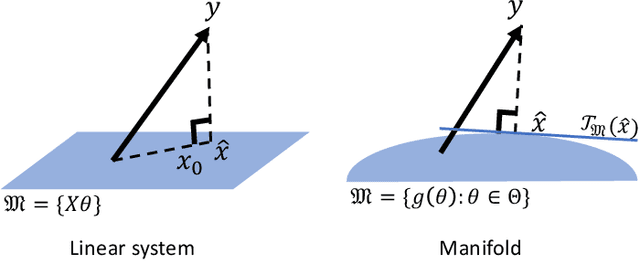
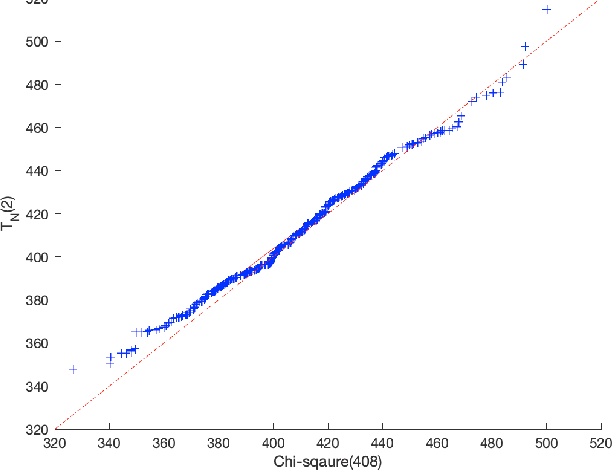
We develop a general theory for the goodness-of-fit test to non-linear models. In particular, we assume that the observations are noisy samples of a sub-manifold defined by a non-linear map of some intrinsic structures. The observation noise is additive Gaussian. Our main result shows that the "residual" of the model fit, by solving a non-linear least-square problem, follows a (possibly non-central) $\chi^2$ distribution. The parameters of the $\chi^2$ distribution are related to the model order and dimension of the problem. The main result is established by making a novel connection between statistical test and differential geometry. We further present a method to select the model orders sequentially. We demonstrate the broad application of the general theory in a range of applications in machine learning and signal processing, including determining the rank of low-rank (possibly complex-valued) matrices and tensors, from noisy, partial, or indirect observations, determining the number of sources in signal demixing, and potential applications in determining the number of hidden nodes in neural networks.

Matrix completion with deterministic pattern - a geometric perspective

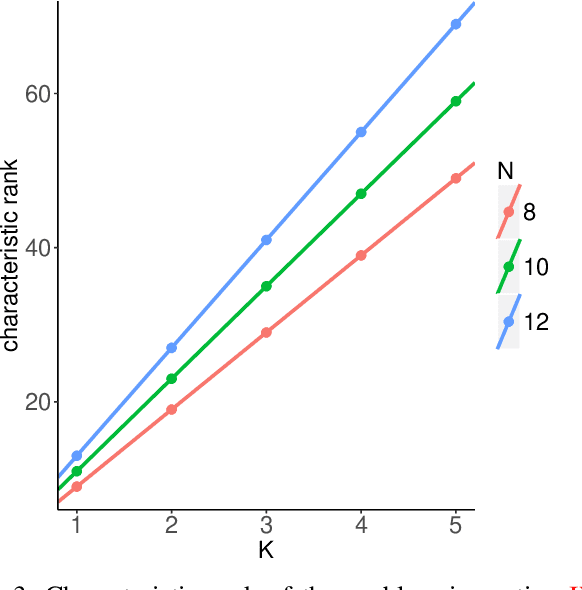
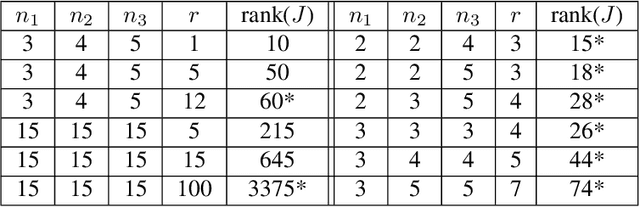
We consider the matrix completion problem with a deterministic pattern of observed entries. In this setting, we aim to answer the question: under what condition there will be (at least locally) unique solution to the matrix completion problem, i.e., the underlying true matrix is identifiable. We answer the question from a certain point of view and outline a geometric perspective. We give an algebraically verifiable sufficient condition, which we call the well-posedness condition, for the local uniqueness of MRMC solutions. We argue that this condition is necessary for local stability of MRMC solutions, and we show that the condition is generic using the characteristic rank. We also argue that the low-rank approximation approaches are more stable than MRMC and further propose a sequential statistical testing procedure to determine the "true" rank from observed entries. Finally, we provide numerical examples aimed at verifying validity of the presented theory.