Goodness-of-fit tests on manifolds

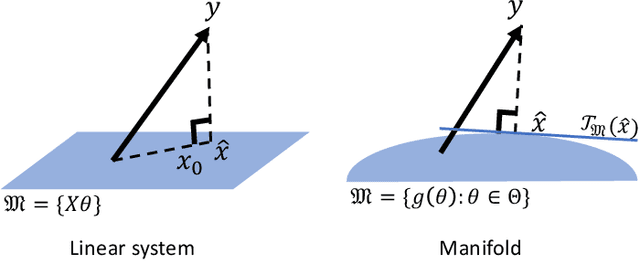
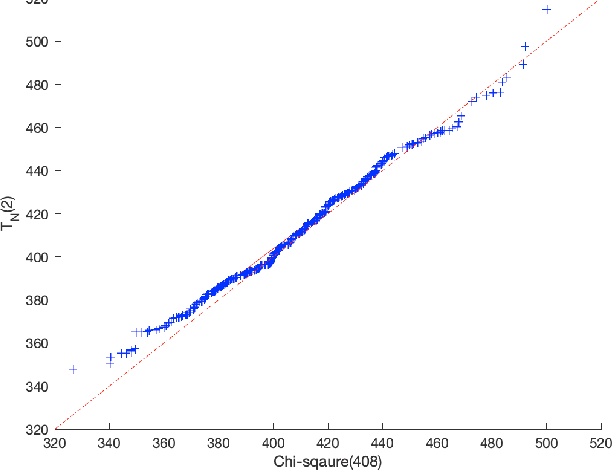
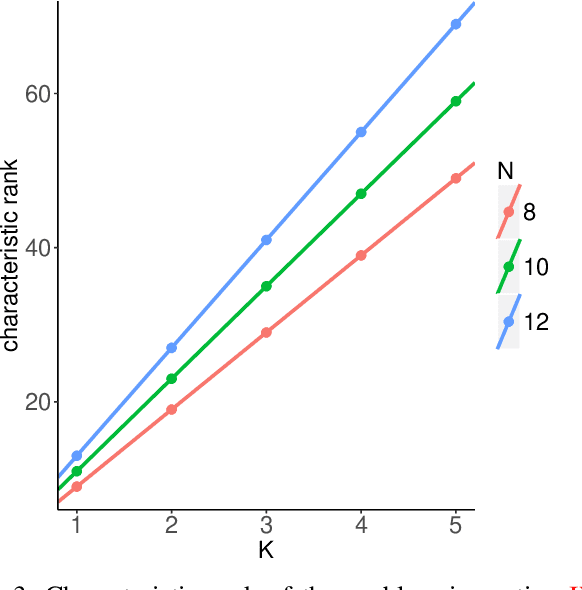
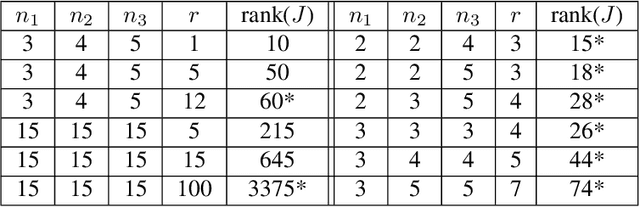
We develop a general theory for the goodness-of-fit test to non-linear models. In particular, we assume that the observations are noisy samples of a sub-manifold defined by a non-linear map of some intrinsic structures. The observation noise is additive Gaussian. Our main result shows that the "residual" of the model fit, by solving a non-linear least-square problem, follows a (possibly non-central) $\chi^2$ distribution. The parameters of the $\chi^2$ distribution are related to the model order and dimension of the problem. The main result is established by making a novel connection between statistical test and differential geometry. We further present a method to select the model orders sequentially. We demonstrate the broad application of the general theory in a range of applications in machine learning and signal processing, including determining the rank of low-rank (possibly complex-valued) matrices and tensors, from noisy, partial, or indirect observations, determining the number of sources in signal demixing, and potential applications in determining the number of hidden nodes in neural networks.