Optimal Sequential Recommendations: Exploiting User and Item Structure

We consider an online model for recommendation systems, with each user being recommended an item at each time-step and providing 'like' or 'dislike' feedback. A latent variable model specifies the user preferences: both users and items are clustered into types. The model captures structure in both the item and user spaces, as used by item-item and user-user collaborative filtering algorithms. We study the situation in which the type preference matrix has i.i.d. entries. Our main contribution is an algorithm that simultaneously uses both item and user structures, proved to be near-optimal via corresponding information-theoretic lower bounds. In particular, our analysis highlights the sub-optimality of using only one of item or user structure (as is done in most collaborative filtering algorithms).

Efficient reductions between some statistical models

We study the problem of approximately transforming a sample from a source statistical model to a sample from a target statistical model without knowing the parameters of the source model, and construct several computationally efficient such reductions between statistical experiments. In particular, we provide computationally efficient procedures that approximately reduce uniform, Erlang, and Laplace location models to general target families. We illustrate our methodology by establishing nonasymptotic reductions between some canonical high-dimensional problems, spanning mixtures of experts, phase retrieval, and signal denoising. Notably, the reductions are structure preserving and can accommodate missing data. We also point to a possible application in transforming one differentially private mechanism to another.

The staircase property: How hierarchical structure can guide deep learning

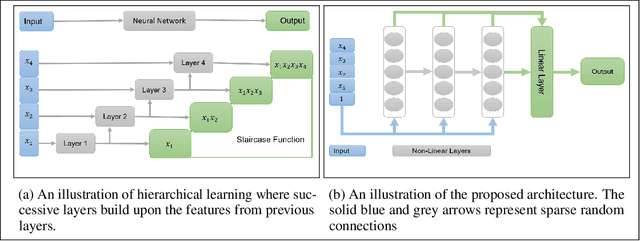
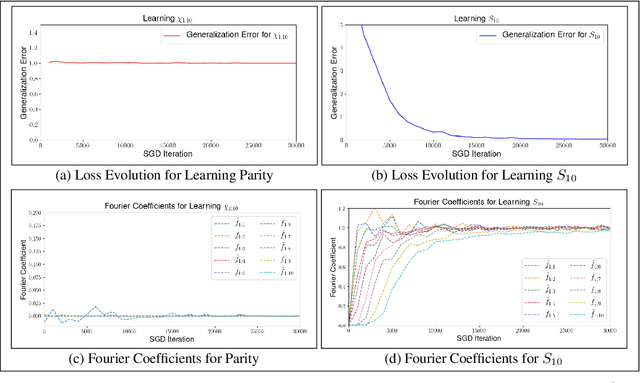
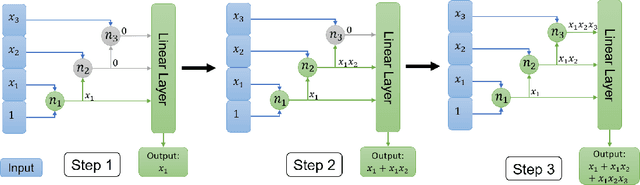
This paper identifies a structural property of data distributions that enables deep neural networks to learn hierarchically. We define the "staircase" property for functions over the Boolean hypercube, which posits that high-order Fourier coefficients are reachable from lower-order Fourier coefficients along increasing chains. We prove that functions satisfying this property can be learned in polynomial time using layerwise stochastic coordinate descent on regular neural networks -- a class of network architectures and initializations that have homogeneity properties. Our analysis shows that for such staircase functions and neural networks, the gradient-based algorithm learns high-level features by greedily combining lower-level features along the depth of the network. We further back our theoretical results with experiments showing that staircase functions are also learnable by more standard ResNet architectures with stochastic gradient descent. Both the theoretical and experimental results support the fact that staircase properties have a role to play in understanding the capabilities of gradient-based learning on regular networks, in contrast to general polynomial-size networks that can emulate any SQ or PAC algorithms as recently shown.

The Algorithmic Phase Transition of Random $k$-SAT for Low Degree Polynomials

Let $\Phi$ be a uniformly random $k$-SAT formula with $n$ variables and $m$ clauses. We study the algorithmic task of finding a satisfying assignment of $\Phi$. It is known that a satisfying assignment exists with high probability at clause density $m/n < 2^k \log 2 - \frac{1}{2} (\log 2 + 1) + o_k(1)$, while the best polynomial-time algorithm known, the Fix algorithm of Coja-Oghlan, finds a satisfying assignment at the much lower clause density $(1 - o_k(1)) 2^k \log k / k$. This prompts the question: is it possible to efficiently find a satisfying assignment at higher clause densities? To understand the algorithmic threshold of random $k$-SAT, we study low degree polynomial algorithms, which are a powerful class of algorithms including Fix, Survey Propagation guided decimation (with bounded or mildly growing number of message passing rounds), and paradigms such as message passing and local graph algorithms. We show that low degree polynomial algorithms can find a satisfying assignment at clause density $(1 - o_k(1)) 2^k \log k / k$, matching Fix, and not at clause density $(1 + o_k(1)) \kappa^* 2^k \log k / k$, where $\kappa^* \approx 4.911$. This shows the first sharp (up to constant factor) computational phase transition of random $k$-SAT for a class of algorithms. Our proof establishes and leverages a new many-way overlap gap property tailored to random $k$-SAT.

Chow-Liu++: Optimal Prediction-Centric Learning of Tree Ising Models

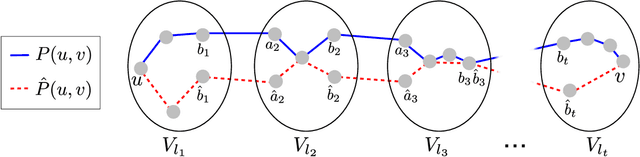
We consider the problem of learning a tree-structured Ising model from data, such that subsequent predictions computed using the model are accurate. Concretely, we aim to learn a model such that posteriors $P(X_i|X_S)$ for small sets of variables $S$ are accurate. Since its introduction more than 50 years ago, the Chow-Liu algorithm, which efficiently computes the maximum likelihood tree, has been the benchmark algorithm for learning tree-structured graphical models. A bound on the sample complexity of the Chow-Liu algorithm with respect to the prediction-centric local total variation loss was shown in [BK19]. While those results demonstrated that it is possible to learn a useful model even when recovering the true underlying graph is impossible, their bound depends on the maximum strength of interactions and thus does not achieve the information-theoretic optimum. In this paper, we introduce a new algorithm that carefully combines elements of the Chow-Liu algorithm with tree metric reconstruction methods to efficiently and optimally learn tree Ising models under a prediction-centric loss. Our algorithm is robust to model misspecification and adversarial corruptions. In contrast, we show that the celebrated Chow-Liu algorithm can be arbitrarily suboptimal.

The EM Algorithm is Adaptively-Optimal for Unbalanced Symmetric Gaussian Mixtures

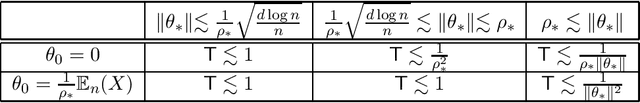
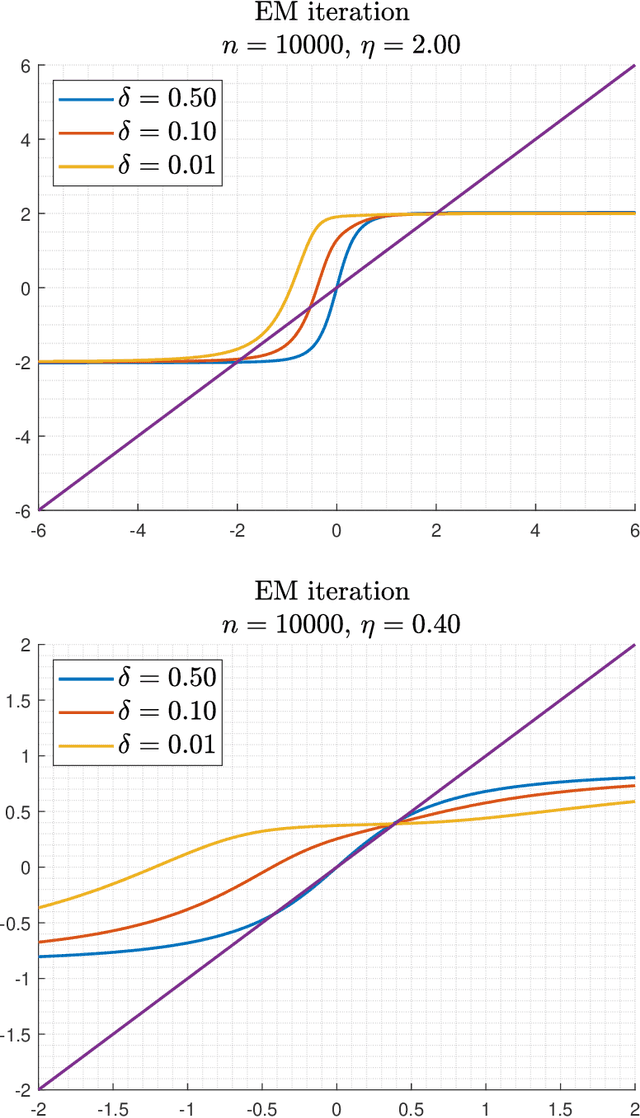
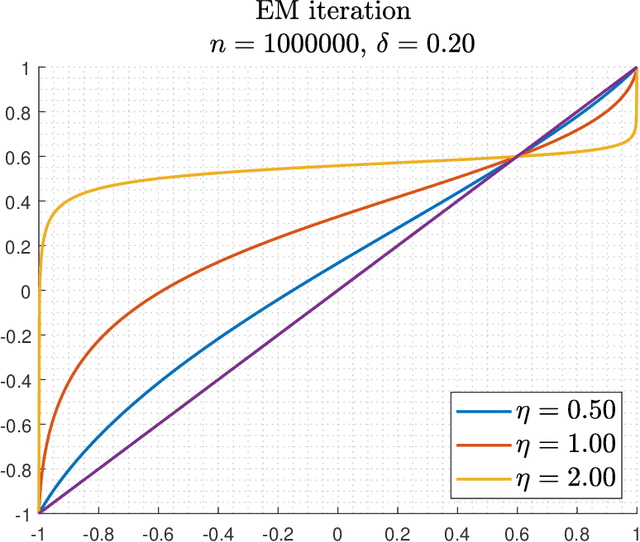
This paper studies the problem of estimating the means $\pm\theta_{*}\in\mathbb{R}^{d}$ of a symmetric two-component Gaussian mixture $\delta_{*}\cdot N(\theta_{*},I)+(1-\delta_{*})\cdot N(-\theta_{*},I)$ where the weights $\delta_{*}$ and $1-\delta_{*}$ are unequal. Assuming that $\delta_{*}$ is known, we show that the population version of the EM algorithm globally converges if the initial estimate has non-negative inner product with the mean of the larger weight component. This can be achieved by the trivial initialization $\theta_{0}=0$. For the empirical iteration based on $n$ samples, we show that when initialized at $\theta_{0}=0$, the EM algorithm adaptively achieves the minimax error rate $\tilde{O}\Big(\min\Big\{\frac{1}{(1-2\delta_{*})}\sqrt{\frac{d}{n}},\frac{1}{\|\theta_{*}\|}\sqrt{\frac{d}{n}},\left(\frac{d}{n}\right)^{1/4}\Big\}\Big)$ in no more than $O\Big(\frac{1}{\|\theta_{*}\|(1-2\delta_{*})}\Big)$ iterations (with high probability). We also consider the EM iteration for estimating the weight $\delta_{*}$, assuming a fixed mean $\theta$ (which is possibly mismatched to $\theta_{*}$). For the empirical iteration of $n$ samples, we show that the minimax error rate $\tilde{O}\Big(\frac{1}{\|\theta_{*}\|}\sqrt{\frac{d}{n}}\Big)$ is achieved in no more than $O\Big(\frac{1}{\|\theta_{*}\|^{2}}\Big)$ iterations. These results robustify and complement recent results of Wu and Zhou obtained for the equal weights case $\delta_{*}=1/2$.

Statistical Query Algorithms and Low-Degree Tests Are Almost Equivalent

Researchers currently use a number of approaches to predict and substantiate information-computation gaps in high-dimensional statistical estimation problems. A prominent approach is to characterize the limits of restricted models of computation, which on the one hand yields strong computational lower bounds for powerful classes of algorithms and on the other hand helps guide the development of efficient algorithms. In this paper, we study two of the most popular restricted computational models, the statistical query framework and low-degree polynomials, in the context of high-dimensional hypothesis testing. Our main result is that under mild conditions on the testing problem, the two classes of algorithms are essentially equivalent in power. As corollaries, we obtain new statistical query lower bounds for sparse PCA, tensor PCA and several variants of the planted clique problem.

Least Squares Regression with Markovian Data: Fundamental Limits and Algorithms

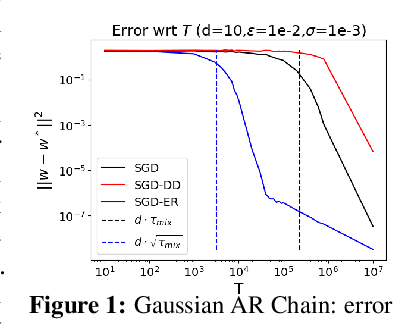
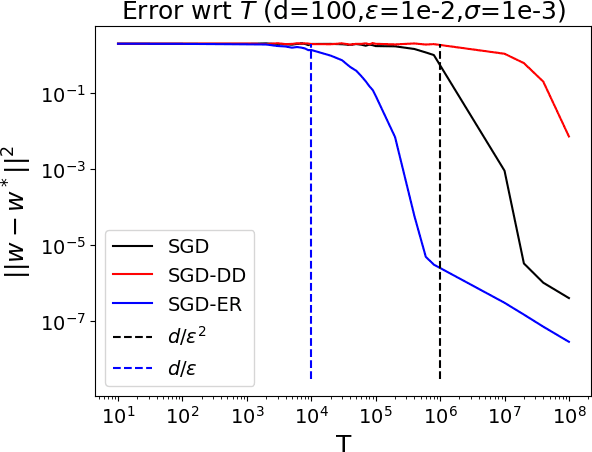
We study the problem of least squares linear regression where the data-points are dependent and are sampled from a Markov chain. We establish sharp information theoretic minimax lower bounds for this problem in terms of $\tau_{\mathsf{mix}}$, the mixing time of the underlying Markov chain, under different noise settings. Our results establish that in general, optimization with Markovian data is strictly harder than optimization with independent data and a trivial algorithm (SGD-DD) that works with only one in every $\tilde{\Theta}(\tau_{\mathsf{mix}})$ samples, which are approximately independent, is minimax optimal. In fact, it is strictly better than the popular Stochastic Gradient Descent (SGD) method with constant step-size which is otherwise minimax optimal in the regression with independent data setting. Beyond a worst case analysis, we investigate whether structured datasets seen in practice such as Gaussian auto-regressive dynamics can admit more efficient optimization schemes. Surprisingly, even in this specific and natural setting, Stochastic Gradient Descent (SGD) with constant step-size is still no better than SGD-DD. Instead, we propose an algorithm based on experience replay--a popular reinforcement learning technique--that achieves a significantly better error rate. Our improved rate serves as one of the first results where an algorithm outperforms SGD-DD on an interesting Markov chain and also provides one of the first theoretical analyses to support the use of experience replay in practice.

Learning Restricted Boltzmann Machines with Few Latent Variables

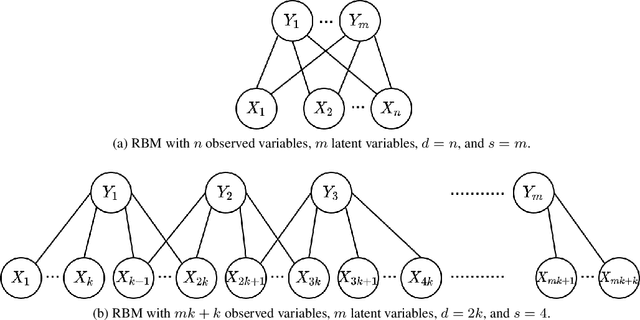
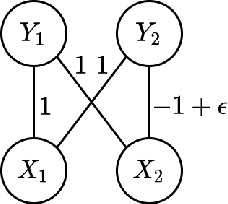
Restricted Boltzmann Machines (RBMs) are a common family of undirected graphical models with latent variables. An RBM is described by a bipartite graph, with all observed variables in one layer and all latent variables in the other. We consider the task of learning an RBM given samples generated according to it. The best algorithms for this task currently have time complexity $\tilde{O}(n^2)$ for ferromagnetic RBMs (i.e., with attractive potentials) but $\tilde{O}(n^d)$ for general RBMs, where $n$ is the number of observed variables and $d$ is the maximum degree of a latent variable. Let the MRF neighborhood of an observed variable be its neighborhood in the Markov Random Field of the marginal distribution of the observed variables. In this paper, we give an algorithm for learning general RBMs with time complexity $\tilde{O}(n^{2^s+1})$, where $s$ is the maximum number of latent variables connected to the MRF neighborhood of an observed variable. This represents an improvement when $s < \log_2 (d-1)$, which is satisfied by many classes of RBMs with "few latent variables''. Furthermore, we give a version of this learning algorithm that recovers a model with small prediction error and whose sample complexity is independent of the minimum potential in the Markov Random Field of the observed variables. This is of interest because the sample complexity of current algorithms scales with the inverse of the minimum potential, which cannot be controlled in terms of natural properties of the RBM.

Sharp Representation Theorems for ReLU Networks with Precise Dependence on Depth

We prove sharp dimension-free representation results for neural networks with $D$ ReLU layers under square loss for a class of functions $\mathcal{G}_D$ defined in the paper. These results capture the precise benefits of depth in the following sense: 1. The rates for representing the class of functions $\mathcal{G}_D$ via $D$ ReLU layers is sharp up to constants, as shown by matching lower bounds. 2. For each $D$, $\mathcal{G}_{D} \subseteq \mathcal{G}_{D+1}$ and as $D$ grows the class of functions $\mathcal{G}_{D}$ contains progressively less smooth functions. 3. If $D^{\prime} < D$, then the approximation rate for the class $\mathcal{G}_D$ achieved by depth $D^{\prime}$ networks is strictly worse than that achieved by depth $D$ networks. This constitutes a fine-grained characterization of the representation power of feedforward networks of arbitrary depth $D$ and number of neurons $N$, in contrast to existing representation results which either require $D$ growing quickly with $N$ or assume that the function being represented is highly smooth. In the latter case similar rates can be obtained with a single nonlinear layer. Our results confirm the prevailing hypothesis that deeper networks are better at representing less smooth functions, and indeed, the main technical novelty is to fully exploit the fact that deep networks can produce highly oscillatory functions with few activation functions.