Chow-Liu++: Optimal Prediction-Centric Learning of Tree Ising Models
Paper and Code
Jun 16, 2021
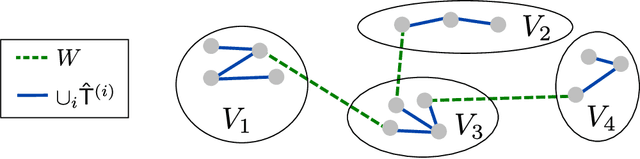
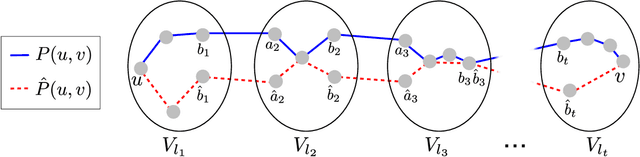
We consider the problem of learning a tree-structured Ising model from data, such that subsequent predictions computed using the model are accurate. Concretely, we aim to learn a model such that posteriors $P(X_i|X_S)$ for small sets of variables $S$ are accurate. Since its introduction more than 50 years ago, the Chow-Liu algorithm, which efficiently computes the maximum likelihood tree, has been the benchmark algorithm for learning tree-structured graphical models. A bound on the sample complexity of the Chow-Liu algorithm with respect to the prediction-centric local total variation loss was shown in [BK19]. While those results demonstrated that it is possible to learn a useful model even when recovering the true underlying graph is impossible, their bound depends on the maximum strength of interactions and thus does not achieve the information-theoretic optimum. In this paper, we introduce a new algorithm that carefully combines elements of the Chow-Liu algorithm with tree metric reconstruction methods to efficiently and optimally learn tree Ising models under a prediction-centric loss. Our algorithm is robust to model misspecification and adversarial corruptions. In contrast, we show that the celebrated Chow-Liu algorithm can be arbitrarily suboptimal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge