The staircase property: How hierarchical structure can guide deep learning

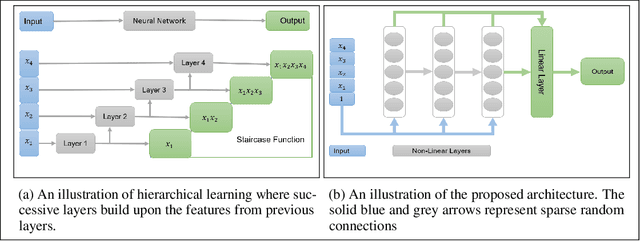
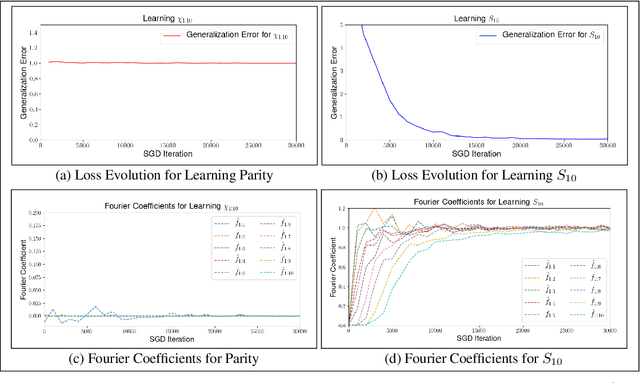
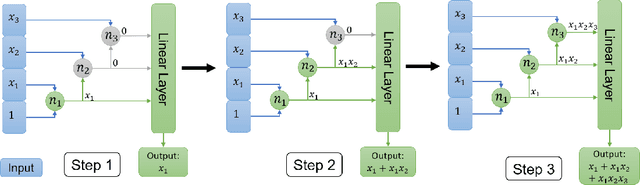
This paper identifies a structural property of data distributions that enables deep neural networks to learn hierarchically. We define the "staircase" property for functions over the Boolean hypercube, which posits that high-order Fourier coefficients are reachable from lower-order Fourier coefficients along increasing chains. We prove that functions satisfying this property can be learned in polynomial time using layerwise stochastic coordinate descent on regular neural networks -- a class of network architectures and initializations that have homogeneity properties. Our analysis shows that for such staircase functions and neural networks, the gradient-based algorithm learns high-level features by greedily combining lower-level features along the depth of the network. We further back our theoretical results with experiments showing that staircase functions are also learnable by more standard ResNet architectures with stochastic gradient descent. Both the theoretical and experimental results support the fact that staircase properties have a role to play in understanding the capabilities of gradient-based learning on regular networks, in contrast to general polynomial-size networks that can emulate any SQ or PAC algorithms as recently shown.

Statistical Query Algorithms and Low-Degree Tests Are Almost Equivalent

Researchers currently use a number of approaches to predict and substantiate information-computation gaps in high-dimensional statistical estimation problems. A prominent approach is to characterize the limits of restricted models of computation, which on the one hand yields strong computational lower bounds for powerful classes of algorithms and on the other hand helps guide the development of efficient algorithms. In this paper, we study two of the most popular restricted computational models, the statistical query framework and low-degree polynomials, in the context of high-dimensional hypothesis testing. Our main result is that under mild conditions on the testing problem, the two classes of algorithms are essentially equivalent in power. As corollaries, we obtain new statistical query lower bounds for sparse PCA, tensor PCA and several variants of the planted clique problem.

Reducibility and Statistical-Computational Gaps from Secret Leakage

Inference problems with conjectured statistical-computational gaps are ubiquitous throughout modern statistics, computer science and statistical physics. While there has been success evidencing these gaps from the failure of restricted classes of algorithms, progress towards a more traditional reduction-based approach to computational complexity in statistical inference has been limited. Existing reductions have largely been limited to inference problems with similar structure -- primarily mapping among problems representable as a sparse submatrix signal plus a noise matrix, which are similar to the common hardness assumption of planted clique. The insight in this work is that a slight generalization of the planted clique conjecture -- secret leakage planted clique -- gives rise to a variety of new average-case reduction techniques, yielding a web of reductions among problems with very different structure. Using variants of the planted clique conjecture for specific forms of secret leakage planted clique, we deduce tight statistical-computational tradeoffs for a diverse range of problems including robust sparse mean estimation, mixtures of sparse linear regressions, robust sparse linear regression, tensor PCA, variants of dense $k$-block stochastic block models, negatively correlated sparse PCA, semirandom planted dense subgraph, detection in hidden partition models and a universality principle for learning sparse mixtures. In particular, a $k$-partite hypergraph variant of the planted clique conjecture is sufficient to establish all of our computational lower bounds. Our techniques also reveal novel connections to combinatorial designs and to random matrix theory. This work gives the first evidence that an expanded set of hardness assumptions, such as for secret leakage planted clique, may be a key first step towards a more complete theory of reductions among statistical problems.

Average-Case Lower Bounds for Learning Sparse Mixtures, Robust Estimation and Semirandom Adversaries

This paper develops several average-case reduction techniques to show new hardness results for three central high-dimensional statistics problems, implying a statistical-computational gap induced by robustness, a detection-recovery gap and a universality principle for these gaps. A main feature of our approach is to map to these problems via a common intermediate problem that we introduce, which we call Imbalanced Sparse Gaussian Mixtures. We assume the planted clique conjecture for a version of the planted clique problem where the position of the planted clique is mildly constrained, and from this obtain the following computational lower bounds: (1) a $k$-to-$k^2$ statistical-computational gap for robust sparse mean estimation, providing the first average-case evidence for a conjecture of Li (2017) and Balakrishnan et al. (2017); (2) a tight lower bound for semirandom planted dense subgraph, which shows that a semirandom adversary shifts the detection threshold in planted dense subgraph to the conjectured recovery threshold; and (3) a universality principle for $k$-to-$k^2$ gaps in a broad class of sparse mixture problems that includes many natural formulations such as the spiked covariance model. Our main approach is to introduce several average-case techniques to produce structured and Gaussianized versions of an input graph problem, and then to rotate these high-dimensional Gaussians by matrices carefully constructed from hyperplanes in $\mathbb{F}_r^t$. For our universality result, we introduce a new method to perform an algorithmic change of measure tailored to sparse mixtures. We also provide evidence that the mild promise in our variant of planted clique does not change the complexity of the problem.

Universality of Computational Lower Bounds for Submatrix Detection

In the general submatrix detection problem, the task is to detect the presence of a small $k \times k$ submatrix with entries sampled from a distribution $\mathcal{P}$ in an $n \times n$ matrix of samples from $\mathcal{Q}$. This formulation includes a number of well-studied problems, such as biclustering when $\mathcal{P}$ and $\mathcal{Q}$ are Gaussians and the planted dense subgraph formulation of community detection when the submatrix is a principal minor and $\mathcal{P}$ and $\mathcal{Q}$ are Bernoulli random variables. These problems all seem to exhibit a universal phenomenon: there is a statistical-computational gap depending on $\mathcal{P}$ and $\mathcal{Q}$ between the minimum $k$ at which this task can be solved and the minimum $k$ at which it can be solved in polynomial time. Our main result is to tightly characterize this computational barrier as a tradeoff between $k$ and the KL divergences between $\mathcal{P}$ and $\mathcal{Q}$ through average-case reductions from the planted clique conjecture. These computational lower bounds hold given mild assumptions on $\mathcal{P}$ and $\mathcal{Q}$ arising naturally from classical binary hypothesis testing. Our results recover and generalize the planted clique lower bounds for Gaussian biclustering in Ma-Wu (2015) and Brennan et al. (2018) and for the sparse and general regimes of planted dense subgraph in Hajek et al. (2015) and Brennan et al. (2018). This yields the first universality principle for computational lower bounds obtained through average-case reductions.

Optimal Average-Case Reductions to Sparse PCA: From Weak Assumptions to Strong Hardness

In the past decade, sparse principal component analysis has emerged as an archetypal problem for illustrating statistical-computational tradeoffs. This trend has largely been driven by a line of research aiming to characterize the average-case complexity of sparse PCA through reductions from the planted clique (PC) conjecture - which conjectures that there is no polynomial-time algorithm to detect a planted clique of size $K = o(N^{1/2})$ in $\mathcal{G}(N, \frac{1}{2})$. All previous reductions to sparse PCA either fail to show tight computational lower bounds matching existing algorithms or show lower bounds for formulations of sparse PCA other than its canonical generative model, the spiked covariance model. Also, these lower bounds all quickly degrade with the exponent in the PC conjecture. Specifically, when only given the PC conjecture up to $K = o(N^\alpha)$ where $\alpha < 1/2$, there is no sparsity level $k$ at which these lower bounds remain tight. If $\alpha \le 1/3$ these reductions fail to even show the existence of a statistical-computational tradeoff at any sparsity $k$. We give a reduction from PC that yields the first full characterization of the computational barrier in the spiked covariance model, providing tight lower bounds at all sparsities $k$. We also show the surprising result that weaker forms of the PC conjecture up to clique size $K = o(N^\alpha)$ for any given $\alpha \in (0, 1/2]$ imply tight computational lower bounds for sparse PCA at sparsities $k = o(n^{\alpha/3})$. This shows that even a mild improvement in the signal strength needed by the best known polynomial-time sparse PCA algorithms would imply that the hardness threshold for PC is subpolynomial. This is the first instance of a suboptimal hardness assumption implying optimal lower bounds for another problem in unsupervised learning.