Almost-Optimal Local-Search Methods for Sparse Tensor PCA

Local-search methods are widely employed in statistical applications, yet interestingly, their theoretical foundations remain rather underexplored, compared to other classes of estimators such as low-degree polynomials and spectral methods. Of note, among the few existing results recent studies have revealed a significant "local-computational" gap in the context of a well-studied sparse tensor principal component analysis (PCA), where a broad class of local Markov chain methods exhibits a notable underperformance relative to other polynomial-time algorithms. In this work, we propose a series of local-search methods that provably "close" this gap to the best known polynomial-time procedures in multiple regimes of the model, including and going beyond the previously studied regimes in which the broad family of local Markov chain methods underperforms. Our framework includes: (1) standard greedy and randomized greedy algorithms applied to the (regularized) posterior of the model; and (2) novel random-threshold variants, in which the randomized greedy algorithm accepts a proposed transition if and only if the corresponding change in the Hamiltonian exceeds a random Gaussian threshold-rather that if and only if it is positive, as is customary. The introduction of the random thresholds enables a tight mathematical analysis of the randomized greedy algorithm's trajectory by crucially breaking the dependencies between the iterations, and could be of independent interest to the community.

An Optimized Franz-Parisi Criterion and its Equivalence with SQ Lower Bounds

Bandeira et al. (2022) introduced the Franz-Parisi (FP) criterion for characterizing the computational hard phases in statistical detection problems. The FP criterion, based on an annealed version of the celebrated Franz-Parisi potential from statistical physics, was shown to be equivalent to low-degree polynomial (LDP) lower bounds for Gaussian additive models, thereby connecting two distinct approaches to understanding the computational hardness in statistical inference. In this paper, we propose a refined FP criterion that aims to better capture the geometric ``overlap" structure of statistical models. Our main result establishes that this optimized FP criterion is equivalent to Statistical Query (SQ) lower bounds -- another foundational framework in computational complexity of statistical inference. Crucially, this equivalence holds under a mild, verifiable assumption satisfied by a broad class of statistical models, including Gaussian additive models, planted sparse models, as well as non-Gaussian component analysis (NGCA), single-index (SI) models, and convex truncation detection settings. For instance, in the case of convex truncation tasks, the assumption is equivalent with the Gaussian correlation inequality (Royen, 2014) from convex geometry. In addition to the above, our equivalence not only unifies and simplifies the derivation of several known SQ lower bounds -- such as for the NGCA model (Diakonikolas et al., 2017) and the SI model (Damian et al., 2024) -- but also yields new SQ lower bounds of independent interest, including for the computational gaps in mixed sparse linear regression (Arpino et al., 2023) and convex truncation (De et al., 2023).

On the Hardness of Learning One Hidden Layer Neural Networks

In this work, we consider the problem of learning one hidden layer ReLU neural networks with inputs from $\mathbb{R}^d$. We show that this learning problem is hard under standard cryptographic assumptions even when: (1) the size of the neural network is polynomial in $d$, (2) its input distribution is a standard Gaussian, and (3) the noise is Gaussian and polynomially small in $d$. Our hardness result is based on the hardness of the Continuous Learning with Errors (CLWE) problem, and in particular, is based on the largely believed worst-case hardness of approximately solving the shortest vector problem up to a multiplicative polynomial factor.

Transfer Learning Beyond Bounded Density Ratios

We study the fundamental problem of transfer learning where a learning algorithm collects data from some source distribution $P$ but needs to perform well with respect to a different target distribution $Q$. A standard change of measure argument implies that transfer learning happens when the density ratio $dQ/dP$ is bounded. Yet, prior thought-provoking works by Kpotufe and Martinet (COLT, 2018) and Hanneke and Kpotufe (NeurIPS, 2019) demonstrate cases where the ratio $dQ/dP$ is unbounded, but transfer learning is possible. In this work, we focus on transfer learning over the class of low-degree polynomial estimators. Our main result is a general transfer inequality over the domain $\mathbb{R}^n$, proving that non-trivial transfer learning for low-degree polynomials is possible under very mild assumptions, going well beyond the classical assumption that $dQ/dP$ is bounded. For instance, it always applies if $Q$ is a log-concave measure and the inverse ratio $dP/dQ$ is bounded. To demonstrate the applicability of our inequality, we obtain new results in the settings of: (1) the classical truncated regression setting, where $dQ/dP$ equals infinity, and (2) the more recent out-of-distribution generalization setting for in-context learning linear functions with transformers. We also provide a discrete analogue of our transfer inequality on the Boolean Hypercube $\{-1,1\}^n$, and study its connections with the recent problem of Generalization on the Unseen of Abbe, Bengio, Lotfi and Rizk (ICML, 2023). Our main conceptual contribution is that the maximum influence of the error of the estimator $\widehat{f}-f^*$ under $Q$, $\mathrm{I}_{\max}(\widehat{f}-f^*)$, acts as a sufficient condition for transferability; when $\mathrm{I}_{\max}(\widehat{f}-f^*)$ is appropriately bounded, transfer is possible over the Boolean domain.

Statistical and Computational Phase Transitions in Group Testing

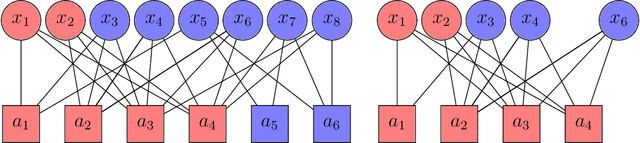
We study the group testing problem where the goal is to identify a set of k infected individuals carrying a rare disease within a population of size n, based on the outcomes of pooled tests which return positive whenever there is at least one infected individual in the tested group. We consider two different simple random procedures for assigning individuals to tests: the constant-column design and Bernoulli design. Our first set of results concerns the fundamental statistical limits. For the constant-column design, we give a new information-theoretic lower bound which implies that the proportion of correctly identifiable infected individuals undergoes a sharp "all-or-nothing" phase transition when the number of tests crosses a particular threshold. For the Bernoulli design, we determine the precise number of tests required to solve the associated detection problem (where the goal is to distinguish between a group testing instance and pure noise), improving both the upper and lower bounds of Truong, Aldridge, and Scarlett (2020). For both group testing models, we also study the power of computationally efficient (polynomial-time) inference procedures. We determine the precise number of tests required for the class of low-degree polynomial algorithms to solve the detection problem. This provides evidence for an inherent computational-statistical gap in both the detection and recovery problems at small sparsity levels. Notably, our evidence is contrary to that of Iliopoulos and Zadik (2021), who predicted the absence of a computational-statistical gap in the Bernoulli design.

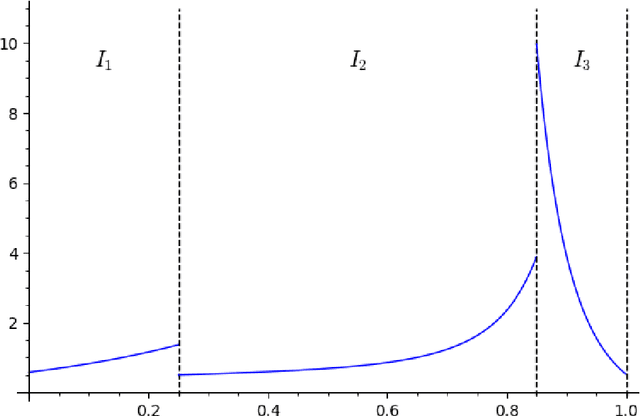
The Franz-Parisi Criterion and Computational Trade-offs in High Dimensional Statistics

Many high-dimensional statistical inference problems are believed to possess inherent computational hardness. Various frameworks have been proposed to give rigorous evidence for such hardness, including lower bounds against restricted models of computation (such as low-degree functions), as well as methods rooted in statistical physics that are based on free energy landscapes. This paper aims to make a rigorous connection between the seemingly different low-degree and free-energy based approaches. We define a free-energy based criterion for hardness and formally connect it to the well-established notion of low-degree hardness for a broad class of statistical problems, namely all Gaussian additive models and certain models with a sparse planted signal. By leveraging these rigorous connections we are able to: establish that for Gaussian additive models the "algebraic" notion of low-degree hardness implies failure of "geometric" local MCMC algorithms, and provide new low-degree lower bounds for sparse linear regression which seem difficult to prove directly. These results provide both conceptual insights into the connections between different notions of hardness, as well as concrete technical tools such as new methods for proving low-degree lower bounds.

Lattice-Based Methods Surpass Sum-of-Squares in Clustering

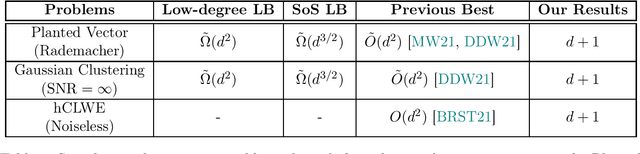
Clustering is a fundamental primitive in unsupervised learning which gives rise to a rich class of computationally-challenging inference tasks. In this work, we focus on the canonical task of clustering d-dimensional Gaussian mixtures with unknown (and possibly degenerate) covariance. Recent works (Ghosh et al. '20; Mao, Wein '21; Davis, Diaz, Wang '21) have established lower bounds against the class of low-degree polynomial methods and the sum-of-squares (SoS) hierarchy for recovering certain hidden structures planted in Gaussian clustering instances. Prior work on many similar inference tasks portends that such lower bounds strongly suggest the presence of an inherent statistical-to-computational gap for clustering, that is, a parameter regime where the clustering task is statistically possible but no polynomial-time algorithm succeeds. One special case of the clustering task we consider is equivalent to the problem of finding a planted hypercube vector in an otherwise random subspace. We show that, perhaps surprisingly, this particular clustering model does not exhibit a statistical-to-computational gap, even though the aforementioned low-degree and SoS lower bounds continue to apply in this case. To achieve this, we give a polynomial-time algorithm based on the Lenstra--Lenstra--Lovasz lattice basis reduction method which achieves the statistically-optimal sample complexity of d+1 samples. This result extends the class of problems whose conjectured statistical-to-computational gaps can be "closed" by "brittle" polynomial-time algorithms, highlighting the crucial but subtle role of noise in the onset of statistical-to-computational gaps.

On the Cryptographic Hardness of Learning Single Periodic Neurons

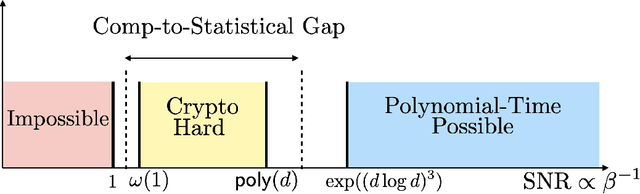
We show a simple reduction which demonstrates the cryptographic hardness of learning a single periodic neuron over isotropic Gaussian distributions in the presence of noise. More precisely, our reduction shows that any polynomial-time algorithm (not necessarily gradient-based) for learning such functions under small noise implies a polynomial-time quantum algorithm for solving worst-case lattice problems, whose hardness form the foundation of lattice-based cryptography. Our core hard family of functions, which are well-approximated by one-layer neural networks, take the general form of a univariate periodic function applied to an affine projection of the data. These functions have appeared in previous seminal works which demonstrate their hardness against gradient-based (Shamir'18), and Statistical Query (SQ) algorithms (Song et al.'17). We show that if (polynomially) small noise is added to the labels, the intractability of learning these functions applies to all polynomial-time algorithms under the aforementioned cryptographic assumptions. Moreover, we demonstrate the necessity of noise in the hardness result by designing a polynomial-time algorithm for learning certain families of such functions under exponentially small adversarial noise. Our proposed algorithm is not a gradient-based or an SQ algorithm, but is rather based on the celebrated Lenstra-Lenstra-Lov\'asz (LLL) lattice basis reduction algorithm. Furthermore, in the absence of noise, this algorithm can be directly applied to solve CLWE detection (Bruna et al.'21) and phase retrieval with an optimal sample complexity of $d+1$ samples. In the former case, this improves upon the quadratic-in-$d$ sample complexity required in (Bruna et al.'21). In the latter case, this improves upon the state-of-the-art AMP-based algorithm, which requires approximately $1.128d$ samples (Barbier et al.'19).

Self-Regularity of Non-Negative Output Weights for Overparameterized Two-Layer Neural Networks

We consider the problem of finding a two-layer neural network with sigmoid, rectified linear unit (ReLU), or binary step activation functions that "fits" a training data set as accurately as possible as quantified by the training error; and study the following question: \emph{does a low training error guarantee that the norm of the output layer (outer norm) itself is small?} We answer affirmatively this question for the case of non-negative output weights. Using a simple covering number argument, we establish that under quite mild distributional assumptions on the input/label pairs; any such network achieving a small training error on polynomially many data necessarily has a well-controlled outer norm. Notably, our results (a) have a polynomial (in $d$) sample complexity, (b) are independent of the number of hidden units (which can potentially be very high), (c) are oblivious to the training algorithm; and (d) require quite mild assumptions on the data (in particular the input vector $X\in\mathbb{R}^d$ need not have independent coordinates). We then leverage our bounds to establish generalization guarantees for such networks through \emph{fat-shattering dimension}, a scale-sensitive measure of the complexity class that the network architectures we investigate belong to. Notably, our generalization bounds also have good sample complexity (polynomials in $d$ with a low degree), and are in fact near-linear for some important cases of interest.

Free Energy Wells and Overlap Gap Property in Sparse PCA

We study a variant of the sparse PCA (principal component analysis) problem in the "hard" regime, where the inference task is possible yet no polynomial-time algorithm is known to exist. Prior work, based on the low-degree likelihood ratio, has conjectured a precise expression for the best possible (sub-exponential) runtime throughout the hard regime. Following instead a statistical physics inspired point of view, we show bounds on the depth of free energy wells for various Gibbs measures naturally associated to the problem. These free energy wells imply hitting time lower bounds that corroborate the low-degree conjecture: we show that a class of natural MCMC (Markov chain Monte Carlo) methods (with worst-case initialization) cannot solve sparse PCA with less than the conjectured runtime. These lower bounds apply to a wide range of values for two tuning parameters: temperature and sparsity misparametrization. Finally, we prove that the Overlap Gap Property (OGP), a structural property that implies failure of certain local search algorithms, holds in a significant part of the hard regime.