Barriers for the performance of graph neural networks in discrete random structures. A comment on~\cite{schuetz2022combinatorial},\cite{angelini2023modern},\cite{schuetz2023reply}

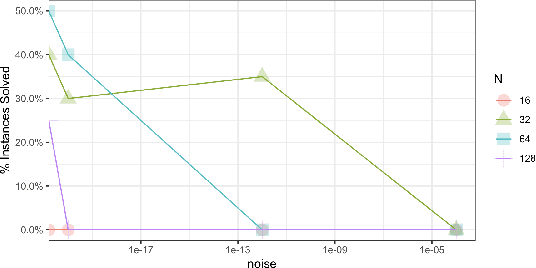
Recently graph neural network (GNN) based algorithms were proposed to solve a variety of combinatorial optimization problems, including Maximum Cut problem, Maximum Independent Set problem and similar other problems~\cite{schuetz2022combinatorial},\cite{schuetz2022graph}. The publication~\cite{schuetz2022combinatorial} stirred a debate whether GNN based method was adequately benchmarked against best prior methods. In particular, critical commentaries~\cite{angelini2023modern} and~\cite{boettcher2023inability} point out that simple greedy algorithm performs better than GNN in the setting of random graphs, and in fact stronger algorithmic performance can be reached with more sophisticated methods. A response from the authors~\cite{schuetz2023reply} pointed out that GNN performance can be improved further by tuning up the parameters better. We do not intend to discuss the merits of arguments and counter-arguments in~\cite{schuetz2022combinatorial},\cite{angelini2023modern},\cite{boettcher2023inability},\cite{schuetz2023reply}. Rather in this note we establish a fundamental limitation for running GNN on random graphs considered in these references, for a broad range of choices of GNN architecture. These limitations arise from the presence of the Overlap Gap Property (OGP) phase transition, which is a barrier for many algorithms, both classical and quantum. As we demonstrate in this paper, it is also a barrier to GNN due to its local structure. We note that at the same time known algorithms ranging from simple greedy algorithms to more sophisticated algorithms based on message passing, provide best results for these problems \emph{up to} the OGP phase transition. This leaves very little space for GNN to outperform the known algorithms, and based on this we side with the conclusions made in~\cite{angelini2023modern} and~\cite{boettcher2023inability}.

Self-Regularity of Non-Negative Output Weights for Overparameterized Two-Layer Neural Networks

We consider the problem of finding a two-layer neural network with sigmoid, rectified linear unit (ReLU), or binary step activation functions that "fits" a training data set as accurately as possible as quantified by the training error; and study the following question: \emph{does a low training error guarantee that the norm of the output layer (outer norm) itself is small?} We answer affirmatively this question for the case of non-negative output weights. Using a simple covering number argument, we establish that under quite mild distributional assumptions on the input/label pairs; any such network achieving a small training error on polynomially many data necessarily has a well-controlled outer norm. Notably, our results (a) have a polynomial (in $d$) sample complexity, (b) are independent of the number of hidden units (which can potentially be very high), (c) are oblivious to the training algorithm; and (d) require quite mild assumptions on the data (in particular the input vector $X\in\mathbb{R}^d$ need not have independent coordinates). We then leverage our bounds to establish generalization guarantees for such networks through \emph{fat-shattering dimension}, a scale-sensitive measure of the complexity class that the network architectures we investigate belong to. Notably, our generalization bounds also have good sample complexity (polynomials in $d$ with a low degree), and are in fact near-linear for some important cases of interest.

Low-Degree Hardness of Random Optimization Problems

We consider the problem of finding nearly optimal solutions of optimization problems with random objective functions. Such problems arise widely in the theory of random graphs, theoretical computer science, and statistical physics. Two concrete problems we consider are (a) optimizing the Hamiltonian of a spherical or Ising p-spin glass model, and (b) finding a large independent set in a sparse Erdos-Renyi graph. Two families of algorithms are considered: (a) low-degree polynomials of the input---a general framework that captures methods such as approximate message passing and local algorithms on sparse graphs, among others; and (b) the Langevin dynamics algorithm, a canonical Monte Carlo analogue of the gradient descent algorithm (applicable only for the spherical p-spin glass Hamiltonian). We show that neither family of algorithms can produce nearly optimal solutions with high probability. Our proof uses the fact that both models are known to exhibit a variant of the overlap gap property (OGP) of near-optimal solutions. Specifically, for both models, every two solutions whose objectives are above a certain threshold are either close or far from each other. The crux of our proof is the stability of both algorithms: a small perturbation of the input induces a small perturbation of the output. By an interpolation argument, such a stable algorithm cannot overcome the OGP barrier. The stability of the Langevin dynamics is an immediate consequence of the well-posedness of stochastic differential equations. The stability of low-degree polynomials is established using concepts from Gaussian and Boolean Fourier analysis, including noise sensitivity, hypercontractivity, and total influence.

Neural Networks and Polynomial Regression. Demystifying the Overparametrization Phenomena

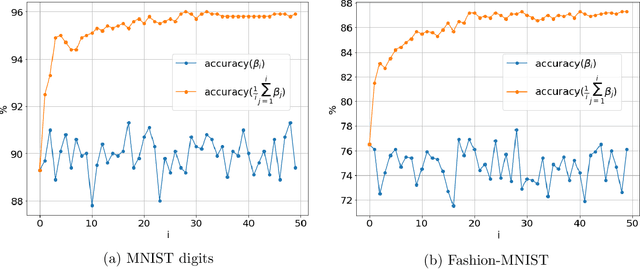
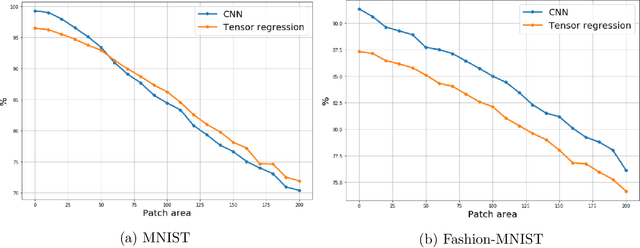
In the context of neural network models, overparametrization refers to the phenomena whereby these models appear to generalize well on the unseen data, even though the number of parameters significantly exceeds the sample sizes, and the model perfectly fits the in-training data. A conventional explanation of this phenomena is based on self-regularization properties of algorithms used to train the data. In this paper we prove a series of results which provide a somewhat diverging explanation. Adopting a teacher/student model where the teacher network is used to generate the predictions and student network is trained on the observed labeled data, and then tested on out-of-sample data, we show that any student network interpolating the data generated by a teacher network generalizes well, provided that the sample size is at least an explicit quantity controlled by data dimension and approximation guarantee alone, regardless of the number of internal nodes of either teacher or student network. Our claim is based on approximating both teacher and student networks by polynomial (tensor) regression models with degree depending on the desired accuracy and network depth only. Such a parametrization notably does not depend on the number of internal nodes. Thus a message implied by our results is that parametrizing wide neural networks by the number of hidden nodes is misleading, and a more fitting measure of parametrization complexity is the number of regression coefficients associated with tensorized data. In particular, this somewhat reconciles the generalization ability of neural networks with more classical statistical notions of data complexity and generalization bounds. Our empirical results on MNIST and Fashion-MNIST datasets indeed confirm that tensorized regression achieves a good out-of-sample performance, even when the degree of the tensor is at most two.

Stationary Points of Shallow Neural Networks with Quadratic Activation Function

We consider the problem of learning shallow neural networks with quadratic activation function and planted weights $W^*\in\mathbb{R}^{m\times d}$, where $m$ is the width of the hidden layer and $d\leqslant m$ is the data dimension. We establish that the landscape of the population risk $\mathcal{L}(W)$ admits an energy barrier separating rank-deficient solutions: if $W\in\mathbb{R}^{m\times d}$ with ${\rm rank}(W)<d$, then $\mathcal{L}(W)\geqslant 2\sigma_{\min}(W^*)^4$, where $\sigma_{\min}(W^*)$ is the smallest singular value of $W^*$. We then establish that all full-rank stationary points of $\mathcal{L}(\cdot)$ are necessarily global optimum. These two results propose a simple explanation for the success of gradient descent in training such networks, when properly initialized: gradient descent algorithm finds global optimum due to absence of spurious stationary points within the set of full-rank matrices. We then show if the planted weight matrix $W^*\in\mathbb{R}^{m\times d}$ has iid Gaussian entries, and is sufficiently wide, that is $m>Cd^2$ for a large $C$, then it is easy to construct a full rank matrix $W$ with population risk below the energy barrier, starting from which gradient descent is guaranteed to converge to a global optimum. Our final focus is on sample complexity: we identify a simple necessary and sufficient geometric condition on the training data under which any minimizer of the empirical loss has necessarily small generalization error. We show that as soon as $n\geqslant n^*=d(d+1)/2$, random data enjoys this geometric condition almost surely, and in fact the generalization error is zero. At the same time we show that if $n<n^*$, then when the data is i.i.d. Gaussian, there always exists a matrix $W$ with zero empirical risk, but with population risk bounded away from zero by the same amount as rank deficient matrices, namely by $2\sigma_{\min}(W^*)^4$.

Inference in High-Dimensional Linear Regression via Lattice Basis Reduction and Integer Relation Detection

We focus on the high-dimensional linear regression problem, where the algorithmic goal is to efficiently infer an unknown feature vector $\beta^*\in\mathbb{R}^p$ from its linear measurements, using a small number $n$ of samples. Unlike most of the literature, we make no sparsity assumption on $\beta^*$, but instead adopt a different regularization: In the noiseless setting, we assume $\beta^*$ consists of entries, which are either rational numbers with a common denominator $Q\in\mathbb{Z}^+$ (referred to as $Q$-rationality); or irrational numbers supported on a rationally independent set of bounded cardinality, known to learner; collectively called as the mixed-support assumption. Using a novel combination of the PSLQ integer relation detection, and LLL lattice basis reduction algorithms, we propose a polynomial-time algorithm which provably recovers a $\beta^*\in\mathbb{R}^p$ enjoying the mixed-support assumption, from its linear measurements $Y=X\beta^*\in\mathbb{R}^n$ for a large class of distributions for the random entries of $X$, even with one measurement $(n=1)$. In the noisy setting, we propose a polynomial-time, lattice-based algorithm, which recovers a $\beta^*\in\mathbb{R}^p$ enjoying $Q$-rationality, from its noisy measurements $Y=X\beta^*+W\in\mathbb{R}^n$, even with a single sample $(n=1)$. We further establish for large $Q$, and normal noise, this algorithm tolerates information-theoretically optimal level of noise. We then apply these ideas to develop a polynomial-time, single-sample algorithm for the phase retrieval problem. Our methods address the single-sample $(n=1)$ regime, where the sparsity-based methods such as LASSO and Basis Pursuit are known to fail. Furthermore, our results also reveal an algorithmic connection between the high-dimensional linear regression problem, and the integer relation detection, randomized subset-sum, and shortest vector problems.

The Landscape of the Planted Clique Problem: Dense subgraphs and the Overlap Gap Property

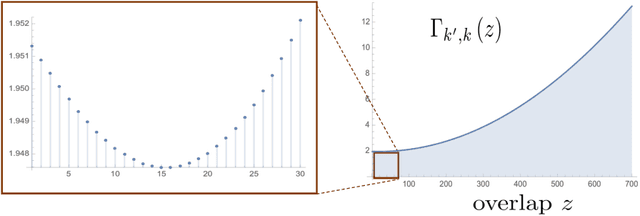
In this paper we study the computational-statistical gap of the planted clique problem, where a clique of size $k$ is planted in an Erdos Renyi graph $G(n,\frac{1}{2})$ resulting in a graph $G\left(n,\frac{1}{2},k\right)$. The goal is to recover the planted clique vertices by observing $G\left(n,\frac{1}{2},k\right)$ . It is known that the clique can be recovered as long as $k \geq \left(2+\epsilon\right)\log n $ for any $\epsilon>0$, but no polynomial-time algorithm is known for this task unless $k=\Omega\left(\sqrt{n} \right)$. Following a statistical-physics inspired point of view as an attempt to understand this computational-statistical gap, we study the landscape of the "sufficiently dense" subgraphs of $G$ and their overlap with the planted clique. Using the first moment method, we study the densest subgraph problems for subgraphs with fixed, but arbitrary, overlap size with the planted clique, and provide evidence of a phase transition for the presence of Overlap Gap Property (OGP) at $k=\Theta\left(\sqrt{n}\right)$. OGP is a concept introduced originally in spin glass theory and known to suggest algorithmic hardness when it appears. We establish the presence of OGP when $k$ is a small positive power of $n$ by using a conditional second moment method. As our main technical tool, we establish the first, to the best of our knowledge, concentration results for the $K$-densest subgraph problem for the Erdos-Renyi model $G\left(n,\frac{1}{2}\right)$ when $K=n^{0.5-\epsilon}$ for arbitrary $\epsilon>0$. Finally, to study the OGP we employ a certain form of overparametrization, which is conceptually aligned with a large body of recent work in learning theory and optimization.

High Dimensional Linear Regression using Lattice Basis Reduction

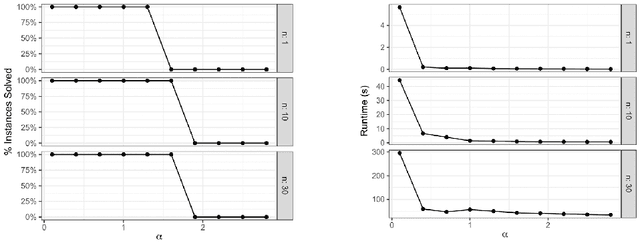
We consider a high dimensional linear regression problem where the goal is to efficiently recover an unknown vector $\beta^*$ from $n$ noisy linear observations $Y=X\beta^*+W \in \mathbb{R}^n$, for known $X \in \mathbb{R}^{n \times p}$ and unknown $W \in \mathbb{R}^n$. Unlike most of the literature on this model we make no sparsity assumption on $\beta^*$. Instead we adopt a regularization based on assuming that the underlying vectors $\beta^*$ have rational entries with the same denominator $Q \in \mathbb{Z}_{>0}$. We call this $Q$-rationality assumption. We propose a new polynomial-time algorithm for this task which is based on the seminal Lenstra-Lenstra-Lovasz (LLL) lattice basis reduction algorithm. We establish that under the $Q$-rationality assumption, our algorithm recovers exactly the vector $\beta^*$ for a large class of distributions for the iid entries of $X$ and non-zero noise $W$. We prove that it is successful under small noise, even when the learner has access to only one observation ($n=1$). Furthermore, we prove that in the case of the Gaussian white noise for $W$, $n=o\left(p/\log p\right)$ and $Q$ sufficiently large, our algorithm tolerates a nearly optimal information-theoretic level of the noise.

Sparse High-Dimensional Linear Regression. Algorithmic Barriers and a Local Search Algorithm

We consider a sparse high dimensional regression model where the goal is to recover a k-sparse unknown vector \beta^* from n noisy linear observations of the form Y=X\beta^*+W \in R^n where X \in R^{n \times p} has iid N(0,1) entries and W \in R^n has iid N(0,\sigma^2) entries. Under certain assumptions on the parameters, an intriguing assymptotic gap appears between the minimum value of n, call it n^*, for which the recovery is information theoretically possible, and the minimum value of n, call it n_{alg}, for which an efficient algorithm is known to provably recover \beta^*. In a recent paper it was conjectured that the gap is not artificial, in the sense that for sample sizes n \in [n^*,n_{alg}] the problem is algorithmically hard. We support this conjecture in two ways. Firstly, we show that a well known recovery mechanism called Basis Pursuit Denoising Scheme provably fails to \ell_2-stably recover the vector when n \in [n^*,c n_{alg}], for some sufficiently small constant c>0. Secondly, we establish that n_{alg}, up to a multiplicative constant factor, is a phase transition point for the appearance of a certain Overlap Gap Property (OGP) over the space of k-sparse vectors. The presence of such an Overlap Gap Property phase transition, which originates in statistical physics, is known to provide evidence of an algorithmic hardness. Finally we show that if n>C n_{alg} for some large enough constant C>0, a very simple algorithm based on a local search improvement is able to infer correctly the support of the unknown vector \beta^*, adding it to the list of provably successful algorithms for the high dimensional linear regression problem.

Matrix Completion from $O$ Samples in Linear Time

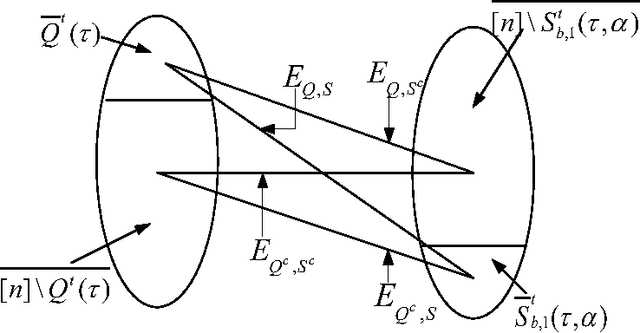
We consider the problem of reconstructing a rank-$k$ $n \times n$ matrix $M$ from a sampling of its entries. Under a certain incoherence assumption on $M$ and for the case when both the rank and the condition number of $M$ are bounded, it was shown in \cite{CandesRecht2009, CandesTao2010, keshavan2010, Recht2011, Jain2012, Hardt2014} that $M$ can be recovered exactly or approximately (depending on some trade-off between accuracy and computational complexity) using $O(n \, \text{poly}(\log n))$ samples in super-linear time $O(n^{a} \, \text{poly}(\log n))$ for some constant $a \geq 1$. In this paper, we propose a new matrix completion algorithm using a novel sampling scheme based on a union of independent sparse random regular bipartite graphs. We show that under the same conditions w.h.p. our algorithm recovers an $\epsilon$-approximation of $M$ in terms of the Frobenius norm using $O(n \log^2(1/\epsilon))$ samples and in linear time $O(n \log^2(1/\epsilon))$. This provides the best known bounds both on the sample complexity and computational complexity for reconstructing (approximately) an unknown low-rank matrix. The novelty of our algorithm is two new steps of thresholding singular values and rescaling singular vectors in the application of the "vanilla" alternating minimization algorithm. The structure of sparse random regular graphs is used heavily for controlling the impact of these regularization steps.