High Dimensional Linear Regression using Lattice Basis Reduction
Paper and Code
Mar 18, 2018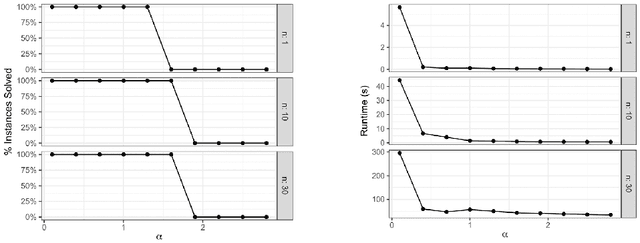
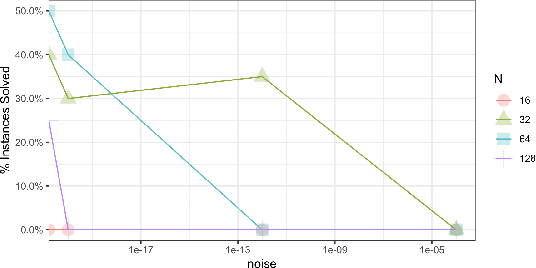
We consider a high dimensional linear regression problem where the goal is to efficiently recover an unknown vector $\beta^*$ from $n$ noisy linear observations $Y=X\beta^*+W \in \mathbb{R}^n$, for known $X \in \mathbb{R}^{n \times p}$ and unknown $W \in \mathbb{R}^n$. Unlike most of the literature on this model we make no sparsity assumption on $\beta^*$. Instead we adopt a regularization based on assuming that the underlying vectors $\beta^*$ have rational entries with the same denominator $Q \in \mathbb{Z}_{>0}$. We call this $Q$-rationality assumption. We propose a new polynomial-time algorithm for this task which is based on the seminal Lenstra-Lenstra-Lovasz (LLL) lattice basis reduction algorithm. We establish that under the $Q$-rationality assumption, our algorithm recovers exactly the vector $\beta^*$ for a large class of distributions for the iid entries of $X$ and non-zero noise $W$. We prove that it is successful under small noise, even when the learner has access to only one observation ($n=1$). Furthermore, we prove that in the case of the Gaussian white noise for $W$, $n=o\left(p/\log p\right)$ and $Q$ sufficiently large, our algorithm tolerates a nearly optimal information-theoretic level of the noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge