Neural Networks and Polynomial Regression. Demystifying the Overparametrization Phenomena
Paper and Code
Mar 23, 2020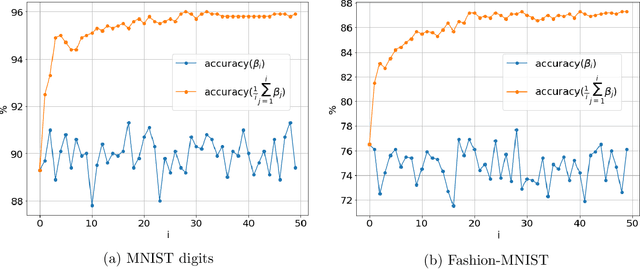


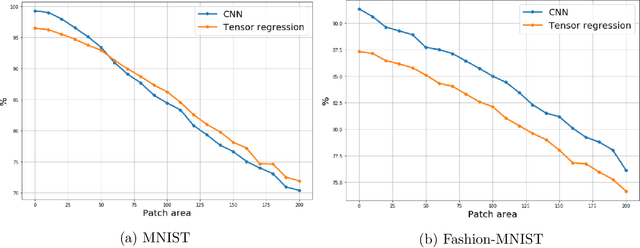
In the context of neural network models, overparametrization refers to the phenomena whereby these models appear to generalize well on the unseen data, even though the number of parameters significantly exceeds the sample sizes, and the model perfectly fits the in-training data. A conventional explanation of this phenomena is based on self-regularization properties of algorithms used to train the data. In this paper we prove a series of results which provide a somewhat diverging explanation. Adopting a teacher/student model where the teacher network is used to generate the predictions and student network is trained on the observed labeled data, and then tested on out-of-sample data, we show that any student network interpolating the data generated by a teacher network generalizes well, provided that the sample size is at least an explicit quantity controlled by data dimension and approximation guarantee alone, regardless of the number of internal nodes of either teacher or student network. Our claim is based on approximating both teacher and student networks by polynomial (tensor) regression models with degree depending on the desired accuracy and network depth only. Such a parametrization notably does not depend on the number of internal nodes. Thus a message implied by our results is that parametrizing wide neural networks by the number of hidden nodes is misleading, and a more fitting measure of parametrization complexity is the number of regression coefficients associated with tensorized data. In particular, this somewhat reconciles the generalization ability of neural networks with more classical statistical notions of data complexity and generalization bounds. Our empirical results on MNIST and Fashion-MNIST datasets indeed confirm that tensorized regression achieves a good out-of-sample performance, even when the degree of the tensor is at most two.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge