Self-Regularity of Non-Negative Output Weights for Overparameterized Two-Layer Neural Networks

We consider the problem of finding a two-layer neural network with sigmoid, rectified linear unit (ReLU), or binary step activation functions that "fits" a training data set as accurately as possible as quantified by the training error; and study the following question: \emph{does a low training error guarantee that the norm of the output layer (outer norm) itself is small?} We answer affirmatively this question for the case of non-negative output weights. Using a simple covering number argument, we establish that under quite mild distributional assumptions on the input/label pairs; any such network achieving a small training error on polynomially many data necessarily has a well-controlled outer norm. Notably, our results (a) have a polynomial (in $d$) sample complexity, (b) are independent of the number of hidden units (which can potentially be very high), (c) are oblivious to the training algorithm; and (d) require quite mild assumptions on the data (in particular the input vector $X\in\mathbb{R}^d$ need not have independent coordinates). We then leverage our bounds to establish generalization guarantees for such networks through \emph{fat-shattering dimension}, a scale-sensitive measure of the complexity class that the network architectures we investigate belong to. Notably, our generalization bounds also have good sample complexity (polynomials in $d$ with a low degree), and are in fact near-linear for some important cases of interest.

Neural Networks and Polynomial Regression. Demystifying the Overparametrization Phenomena

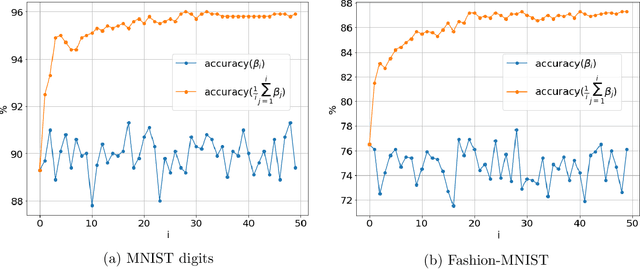
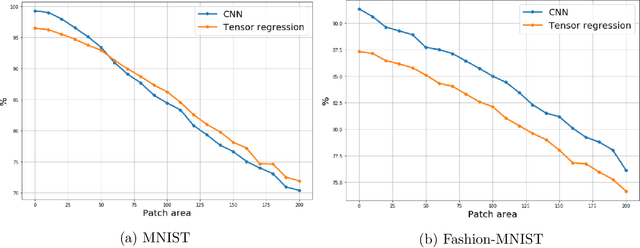
In the context of neural network models, overparametrization refers to the phenomena whereby these models appear to generalize well on the unseen data, even though the number of parameters significantly exceeds the sample sizes, and the model perfectly fits the in-training data. A conventional explanation of this phenomena is based on self-regularization properties of algorithms used to train the data. In this paper we prove a series of results which provide a somewhat diverging explanation. Adopting a teacher/student model where the teacher network is used to generate the predictions and student network is trained on the observed labeled data, and then tested on out-of-sample data, we show that any student network interpolating the data generated by a teacher network generalizes well, provided that the sample size is at least an explicit quantity controlled by data dimension and approximation guarantee alone, regardless of the number of internal nodes of either teacher or student network. Our claim is based on approximating both teacher and student networks by polynomial (tensor) regression models with degree depending on the desired accuracy and network depth only. Such a parametrization notably does not depend on the number of internal nodes. Thus a message implied by our results is that parametrizing wide neural networks by the number of hidden nodes is misleading, and a more fitting measure of parametrization complexity is the number of regression coefficients associated with tensorized data. In particular, this somewhat reconciles the generalization ability of neural networks with more classical statistical notions of data complexity and generalization bounds. Our empirical results on MNIST and Fashion-MNIST datasets indeed confirm that tensorized regression achieves a good out-of-sample performance, even when the degree of the tensor is at most two.

Stationary Points of Shallow Neural Networks with Quadratic Activation Function

We consider the problem of learning shallow neural networks with quadratic activation function and planted weights $W^*\in\mathbb{R}^{m\times d}$, where $m$ is the width of the hidden layer and $d\leqslant m$ is the data dimension. We establish that the landscape of the population risk $\mathcal{L}(W)$ admits an energy barrier separating rank-deficient solutions: if $W\in\mathbb{R}^{m\times d}$ with ${\rm rank}(W)<d$, then $\mathcal{L}(W)\geqslant 2\sigma_{\min}(W^*)^4$, where $\sigma_{\min}(W^*)$ is the smallest singular value of $W^*$. We then establish that all full-rank stationary points of $\mathcal{L}(\cdot)$ are necessarily global optimum. These two results propose a simple explanation for the success of gradient descent in training such networks, when properly initialized: gradient descent algorithm finds global optimum due to absence of spurious stationary points within the set of full-rank matrices. We then show if the planted weight matrix $W^*\in\mathbb{R}^{m\times d}$ has iid Gaussian entries, and is sufficiently wide, that is $m>Cd^2$ for a large $C$, then it is easy to construct a full rank matrix $W$ with population risk below the energy barrier, starting from which gradient descent is guaranteed to converge to a global optimum. Our final focus is on sample complexity: we identify a simple necessary and sufficient geometric condition on the training data under which any minimizer of the empirical loss has necessarily small generalization error. We show that as soon as $n\geqslant n^*=d(d+1)/2$, random data enjoys this geometric condition almost surely, and in fact the generalization error is zero. At the same time we show that if $n<n^*$, then when the data is i.i.d. Gaussian, there always exists a matrix $W$ with zero empirical risk, but with population risk bounded away from zero by the same amount as rank deficient matrices, namely by $2\sigma_{\min}(W^*)^4$.

Inference in High-Dimensional Linear Regression via Lattice Basis Reduction and Integer Relation Detection

We focus on the high-dimensional linear regression problem, where the algorithmic goal is to efficiently infer an unknown feature vector $\beta^*\in\mathbb{R}^p$ from its linear measurements, using a small number $n$ of samples. Unlike most of the literature, we make no sparsity assumption on $\beta^*$, but instead adopt a different regularization: In the noiseless setting, we assume $\beta^*$ consists of entries, which are either rational numbers with a common denominator $Q\in\mathbb{Z}^+$ (referred to as $Q$-rationality); or irrational numbers supported on a rationally independent set of bounded cardinality, known to learner; collectively called as the mixed-support assumption. Using a novel combination of the PSLQ integer relation detection, and LLL lattice basis reduction algorithms, we propose a polynomial-time algorithm which provably recovers a $\beta^*\in\mathbb{R}^p$ enjoying the mixed-support assumption, from its linear measurements $Y=X\beta^*\in\mathbb{R}^n$ for a large class of distributions for the random entries of $X$, even with one measurement $(n=1)$. In the noisy setting, we propose a polynomial-time, lattice-based algorithm, which recovers a $\beta^*\in\mathbb{R}^p$ enjoying $Q$-rationality, from its noisy measurements $Y=X\beta^*+W\in\mathbb{R}^n$, even with a single sample $(n=1)$. We further establish for large $Q$, and normal noise, this algorithm tolerates information-theoretically optimal level of noise. We then apply these ideas to develop a polynomial-time, single-sample algorithm for the phase retrieval problem. Our methods address the single-sample $(n=1)$ regime, where the sparsity-based methods such as LASSO and Basis Pursuit are known to fail. Furthermore, our results also reveal an algorithmic connection between the high-dimensional linear regression problem, and the integer relation detection, randomized subset-sum, and shortest vector problems.