Statistical and Computational Phase Transitions in Group Testing

We study the group testing problem where the goal is to identify a set of k infected individuals carrying a rare disease within a population of size n, based on the outcomes of pooled tests which return positive whenever there is at least one infected individual in the tested group. We consider two different simple random procedures for assigning individuals to tests: the constant-column design and Bernoulli design. Our first set of results concerns the fundamental statistical limits. For the constant-column design, we give a new information-theoretic lower bound which implies that the proportion of correctly identifiable infected individuals undergoes a sharp "all-or-nothing" phase transition when the number of tests crosses a particular threshold. For the Bernoulli design, we determine the precise number of tests required to solve the associated detection problem (where the goal is to distinguish between a group testing instance and pure noise), improving both the upper and lower bounds of Truong, Aldridge, and Scarlett (2020). For both group testing models, we also study the power of computationally efficient (polynomial-time) inference procedures. We determine the precise number of tests required for the class of low-degree polynomial algorithms to solve the detection problem. This provides evidence for an inherent computational-statistical gap in both the detection and recovery problems at small sparsity levels. Notably, our evidence is contrary to that of Iliopoulos and Zadik (2021), who predicted the absence of a computational-statistical gap in the Bernoulli design.

Separating populations with wide data: A spectral analysis

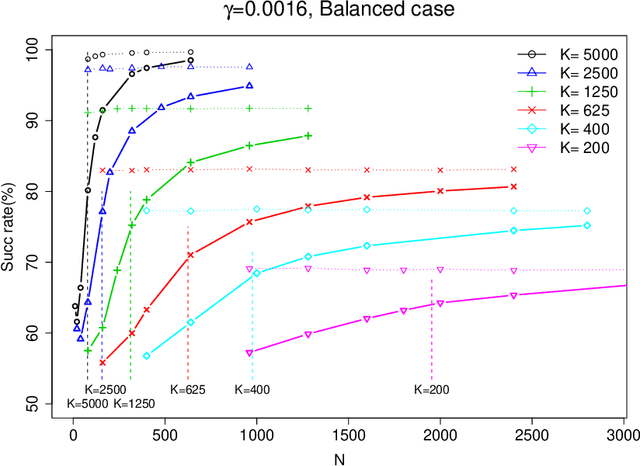
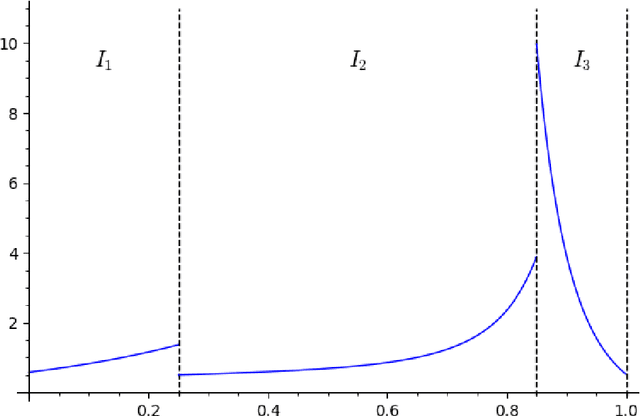
In this paper, we consider the problem of partitioning a small data sample drawn from a mixture of $k$ product distributions. We are interested in the case that individual features are of low average quality $\gamma$, and we want to use as few of them as possible to correctly partition the sample. We analyze a spectral technique that is able to approximately optimize the total data size--the product of number of data points $n$ and the number of features $K$--needed to correctly perform this partitioning as a function of $1/\gamma$ for $K>n$. Our goal is motivated by an application in clustering individuals according to their population of origin using markers, when the divergence between any two of the populations is small.

A Spectral Approach to Analyzing Belief Propagation for 3-Coloring

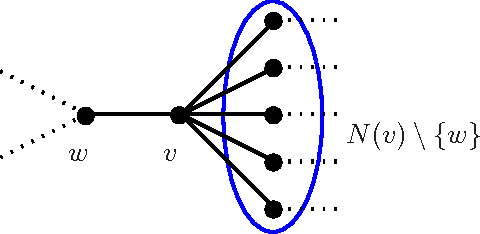
Contributing to the rigorous understanding of BP, in this paper we relate the convergence of BP to spectral properties of the graph. This encompasses a result for random graphs with a ``planted'' solution; thus, we obtain the first rigorous result on BP for graph coloring in the case of a complex graphical structure (as opposed to trees). In particular, the analysis shows how Belief Propagation breaks the symmetry between the $3!$ possible permutations of the color classes.