On a Near-Optimal \& Efficient Algorithm for the Sparse Pooled Data Problem

The pooled data problem asks to identify the unknown labels of a set of items from condensed measurements. More precisely, given $n$ items, assume that each item has a label in $\cbc{0,1,\ldots, d}$, encoded via the ground-truth $\SIGMA$. We call the pooled data problem sparse if the number of non-zero entries of $\SIGMA$ scales as $k \sim n^{\theta}$ for $\theta \in (0,1)$. The information that is revealed about $\SIGMA$ comes from pooled measurements, each indicating how many items of each label are contained in the pool. The most basic question is to design a pooling scheme that uses as few pools as possible, while reconstructing $\SIGMA$ with high probability. Variants of the problem and its combinatorial ramifications have been studied for at least 35 years. However, the study of the modern question of \emph{efficient} inference of the labels has suggested a statistical-to-computational gap of order $\log n$ in the minimum number of pools needed for theoretically possible versus efficient inference. In this article, we resolve the question whether this $\log n$-gap is artificial or of a fundamental nature by the design of an efficient algorithm, called \algoname, based upon a novel pooling scheme on a number of pools very close to the information-theoretic threshold.

An unsupervised learning approach to evaluate questionnaire data -- what one can learn from violations of measurement invariance

In several branches of the social sciences and humanities, surveys based on standardized questionnaires are a prominent research tool. While there are a variety of ways to analyze the data, some standard procedures have become established. When those surveys want to analyze differences in the answer patterns of different groups (e.g., countries, gender, age, ...), these procedures can only be carried out in a meaningful way if there is measurement invariance, i.e., the measured construct has psychometric equivalence across groups. As recently raised as an open problem by Sauerwein et al. (2021), new evaluation methods that work in the absence of measurement invariance are needed. This paper promotes an unsupervised learning-based approach to such research data by proposing a procedure that works in three phases: data preparation, clustering of questionnaires, and measuring similarity based on the obtained clustering and the properties of each group. We generate synthetic data in three data sets, which allows us to compare our approach with the PCA approach under measurement invariance and under violated measurement invariance. As a main result, we obtain that the approach provides a natural comparison between groups and a natural description of the response patterns of the groups. Moreover, it can be safely applied to a wide variety of data sets, even in the absence of measurement invariance. Finally, this approach allows us to translate (violations of) measurement invariance into a meaningful measure of similarity.

A Notion of Feature Importance by Decorrelation and Detection of Trends by Random Forest Regression

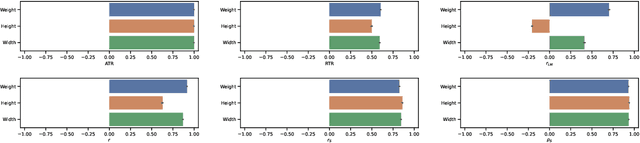
In many studies, we want to determine the influence of certain features on a dependent variable. More specifically, we are interested in the strength of the influence -- i.e., is the feature relevant? -- and, if so, how the feature influences the dependent variable. Recently, data-driven approaches such as \emph{random forest regression} have found their way into applications (Boulesteix et al., 2012). These models allow to directly derive measures of feature importance, which are a natural indicator of the strength of the influence. For the relevant features, the correlation or rank correlation between the feature and the dependent variable has typically been used to determine the nature of the influence. More recent methods, some of which can also measure interactions between features, are based on a modeling approach. In particular, when machine learning models are used, SHAP scores are a recent and prominent method to determine these trends (Lundberg et al., 2017). In this paper, we introduce a novel notion of feature importance based on the well-studied Gram-Schmidt decorrelation method. Furthermore, we propose two estimators for identifying trends in the data using random forest regression, the so-called absolute and relative transversal rate. We empirically compare the properties of our estimators with those of well-established estimators on a variety of synthetic and real-world datasets.

Efficient Approximate Recovery from Pooled Data Using Doubly Regular Pooling Schemes

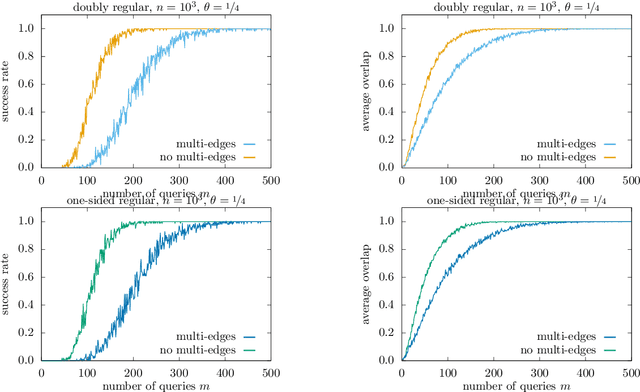
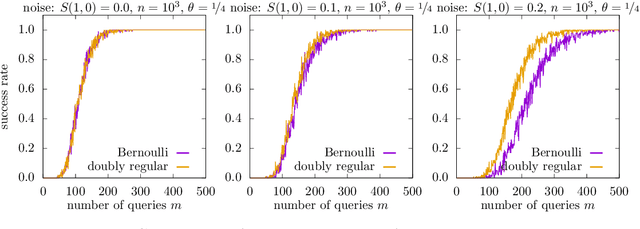
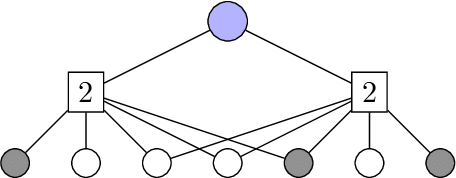
In the pooled data problem we are given $n$ agents with hidden state bits, either $0$ or $1$. The hidden states are unknown and can be seen as the underlying ground truth $\sigma$. To uncover that ground truth, we are given a querying method that queries multiple agents at a time. Each query reports the sum of the states of the queried agents. Our goal is to learn the hidden state bits using as few queries as possible. So far, most literature deals with exact reconstruction of all hidden state bits. We study a more relaxed variant in which we allow a small fraction of agents to be classified incorrectly. This becomes particularly relevant in the noisy variant of the pooled data problem where the queries' results are subject to random noise. In this setting, we provide a doubly regular test design that assigns agents to queries. For this design we analyze an approximate reconstruction algorithm that estimates the hidden bits in a greedy fashion. We give a rigorous analysis of the algorithm's performance, its error probability, and its approximation quality. As a main technical novelty, our analysis is uniform in the degree of noise and the sparsity of $\sigma$. Finally, simulations back up our theoretical findings and provide strong empirical evidence that our algorithm works well for realistic sample sizes.

Statistical and Computational Phase Transitions in Group Testing

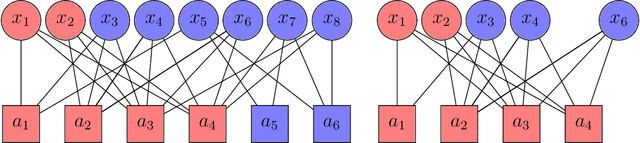
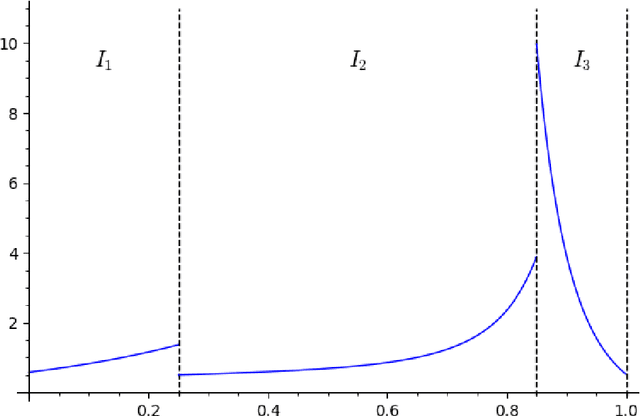
We study the group testing problem where the goal is to identify a set of k infected individuals carrying a rare disease within a population of size n, based on the outcomes of pooled tests which return positive whenever there is at least one infected individual in the tested group. We consider two different simple random procedures for assigning individuals to tests: the constant-column design and Bernoulli design. Our first set of results concerns the fundamental statistical limits. For the constant-column design, we give a new information-theoretic lower bound which implies that the proportion of correctly identifiable infected individuals undergoes a sharp "all-or-nothing" phase transition when the number of tests crosses a particular threshold. For the Bernoulli design, we determine the precise number of tests required to solve the associated detection problem (where the goal is to distinguish between a group testing instance and pure noise), improving both the upper and lower bounds of Truong, Aldridge, and Scarlett (2020). For both group testing models, we also study the power of computationally efficient (polynomial-time) inference procedures. We determine the precise number of tests required for the class of low-degree polynomial algorithms to solve the detection problem. This provides evidence for an inherent computational-statistical gap in both the detection and recovery problems at small sparsity levels. Notably, our evidence is contrary to that of Iliopoulos and Zadik (2021), who predicted the absence of a computational-statistical gap in the Bernoulli design.

Inference of a Rumor's Source in the Independent Cascade Model

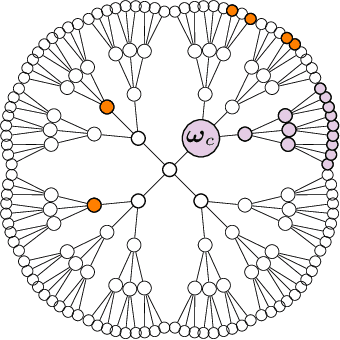
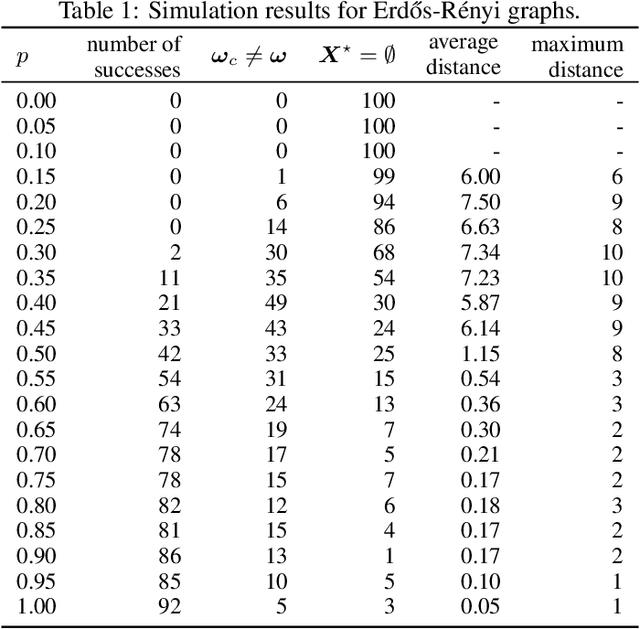
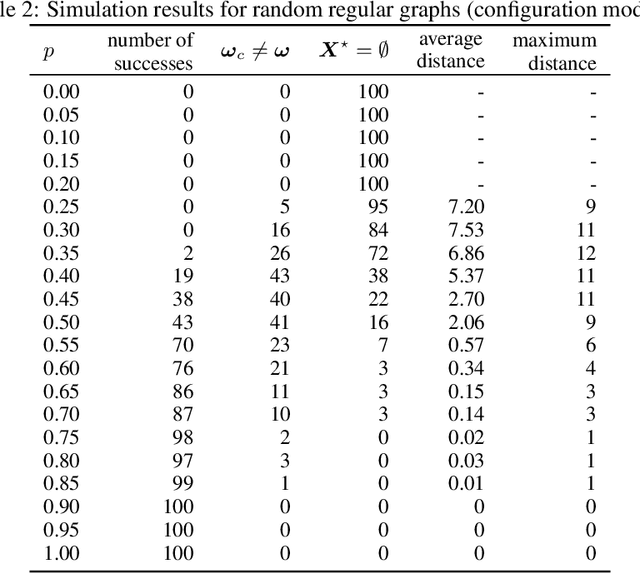
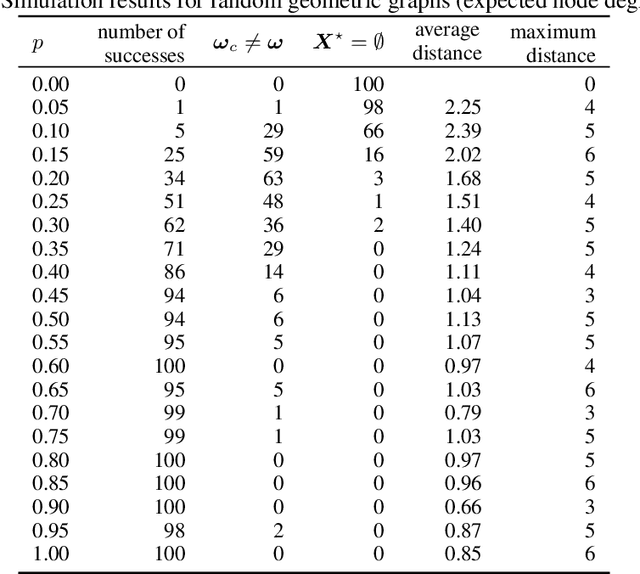
We consider the so-called Independent Cascade Model for rumor spreading or epidemic processes popularized by Kempe et al.\ [2003]. In this model, a small subset of nodes from a network are the source of a rumor. In discrete time steps, each informed node "infects" each of its uninformed neighbors with probability $p$. While many facets of this process are studied in the literature, less is known about the inference problem: given a number of infected nodes in a network, can we learn the source of the rumor? In the context of epidemiology this problem is often referred to as patient zero problem. It belongs to a broader class of problems where the goal is to infer parameters of the underlying spreading model, see, e.g., Lokhov [NeurIPS'16] or Mastakouri et al. [NeurIPS'20]. In this work we present a maximum likelihood estimator for the rumor's source, given a snapshot of the process in terms of a set of active nodes $X$ after $t$ steps. Our results show that, for cycle-free graphs, the likelihood estimator undergoes a non-trivial phase transition as a function $t$. We provide a rigorous analysis for two prominent classes of acyclic network, namely $d$-regular trees and Galton-Watson trees, and verify empirically that our heuristics work well in various general networks.

Distributed Reconstruction of Noisy Pooled Data

In the pooled data problem we are given a set of $n$ agents, each of which holds a hidden state bit, either $0$ or $1$. A querying procedure returns for a query set the sum of the states of the queried agents. The goal is to reconstruct the states using as few queries as possible. In this paper we consider two noise models for the pooled data problem. In the noisy channel model, the result for each agent flips with a certain probability. In the noisy query model, each query result is subject to random Gaussian noise. Our results are twofold. First, we present and analyze for both error models a simple and efficient distributed algorithm that reconstructs the initial states in a greedy fashion. Our novel analysis pins down the range of error probabilities and distributions for which our algorithm reconstructs the exact initial states with high probability. Secondly, we present simulation results of our algorithm and compare its performance with approximate message passing (AMP) algorithms that are conjectured to be optimal in a number of related problems.

Efficient and accurate group testing via Belief Propagation: an empirical study

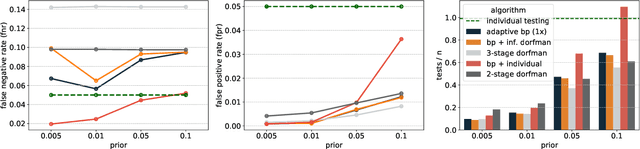
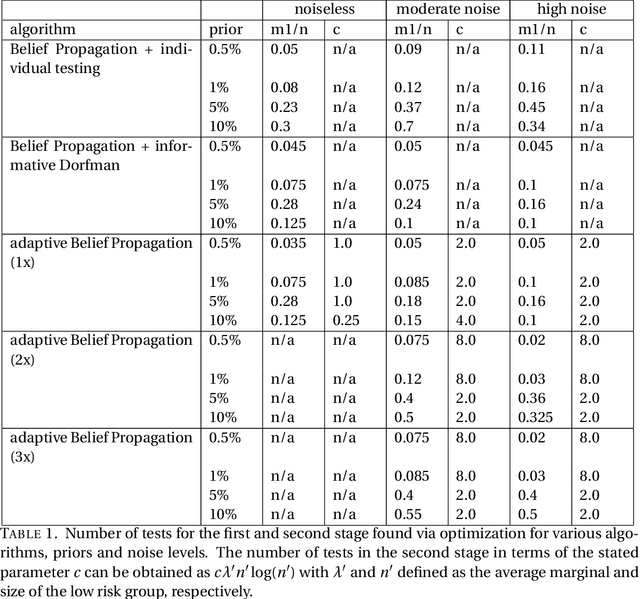
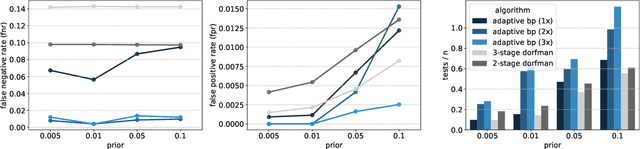
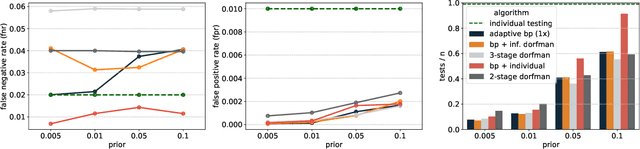
The group testing problem asks for efficient pooling schemes and algorithms that allow to screen moderately large numbers of samples for rare infections. The goal is to accurately identify the infected samples while conducting the least possible number of tests. Exploring the use of techniques centred around the Belief Propagation message passing algorithm, we suggest a new test design that significantly increases the accuracy of the results. The new design comes with Belief Propagation as an efficient inference algorithm. Aiming for results on practical rather than asymptotic problem sizes, we conduct an experimental study.