Remco van der Hofstad
Learning the mechanisms of network growth
Mar 31, 2024Abstract:We propose a novel model-selection method for dynamic real-life networks. Our approach involves training a classifier on a large body of synthetic network data. The data is generated by simulating nine state-of-the-art random graph models for dynamic networks, with parameter range chosen to ensure exponential growth of the network size in time. We design a conceptually novel type of dynamic features that count new links received by a group of vertices in a particular time interval. The proposed features are easy to compute, analytically tractable, and interpretable. Our approach achieves a near-perfect classification of synthetic networks, exceeding the state-of-the-art by a large margin. Applying our classification method to real-world citation networks gives credibility to the claims in the literature that models with preferential attachment, fitness and aging fit real-world citation networks best, although sometimes, the predicted model does not involve vertex fitness.
Communication protocol for a satellite-swarm interferometer
Dec 25, 2023Abstract:Orbiting low frequency antennas for radio astronomy (OLFAR) that capture cosmic signals in the frequency range below 30MHz could provide valuable insights on our Universe. These wireless swarms of satellites form a connectivity graph that allows data exchange between most pairs of satellites. Since this swarm acts as an interferometer, the aim is to compute the cross-correlations between most pairs of satellites. We propose a k-nearest-neighbour communication protocol, and investigate the minimum neighbourhood size of each satellite that ensures connectivity of at least 95% of the swarm. We describe the proportion of cross-correlations that can be computed in our method given an energy budget per satellite. Despite the method's apparent simplicity, it allows us to gain insight into the requirements for such satellite swarms. In particular, we give specific advice on the energy requirements to have sufficient coverage of the relevant baselines.
On a Near-Optimal \& Efficient Algorithm for the Sparse Pooled Data Problem
Dec 22, 2023Abstract:The pooled data problem asks to identify the unknown labels of a set of items from condensed measurements. More precisely, given $n$ items, assume that each item has a label in $\cbc{0,1,\ldots, d}$, encoded via the ground-truth $\SIGMA$. We call the pooled data problem sparse if the number of non-zero entries of $\SIGMA$ scales as $k \sim n^{\theta}$ for $\theta \in (0,1)$. The information that is revealed about $\SIGMA$ comes from pooled measurements, each indicating how many items of each label are contained in the pool. The most basic question is to design a pooling scheme that uses as few pools as possible, while reconstructing $\SIGMA$ with high probability. Variants of the problem and its combinatorial ramifications have been studied for at least 35 years. However, the study of the modern question of \emph{efficient} inference of the labels has suggested a statistical-to-computational gap of order $\log n$ in the minimum number of pools needed for theoretically possible versus efficient inference. In this article, we resolve the question whether this $\log n$-gap is artificial or of a fundamental nature by the design of an efficient algorithm, called \algoname, based upon a novel pooling scheme on a number of pools very close to the information-theoretic threshold.
The Hyperspherical Geometry of Community Detection: Modularity as a Distance
Jul 06, 2021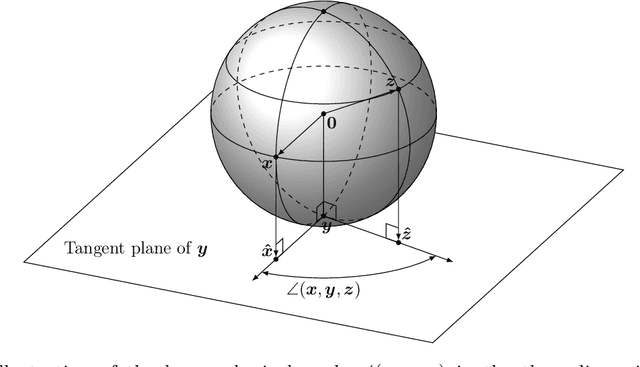
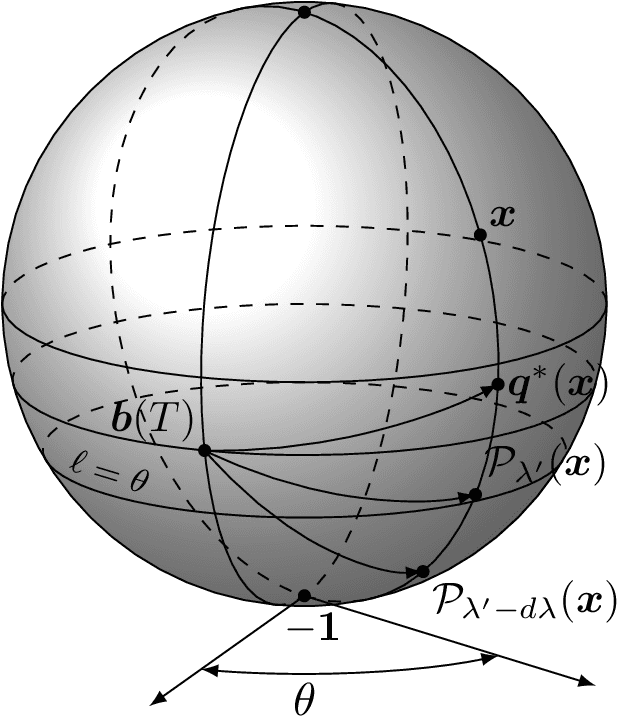
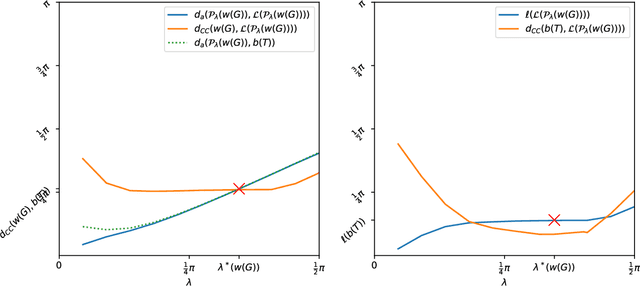
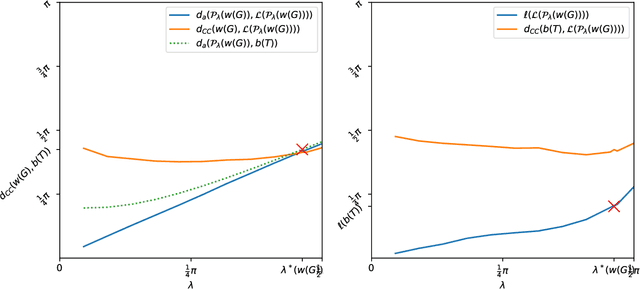
Abstract:The Louvain algorithm is currently one of the most popular community detection methods. This algorithm finds communities by maximizing a quantity called modularity. In this work, we describe a metric space of clusterings, where clusterings are described by a binary vector indexed by the vertex-pairs. We extend this geometry to a hypersphere and prove that maximizing modularity is equivalent to minimizing the angular distance to some modularity vector over the set of clustering vectors. This equivalence allows us to view the Louvain algorithm as a nearest-neighbor search that approximately minimizes the distance to this modularity vector. By replacing this modularity vector by a different vector, many alternative community detection methods can be obtained. We explore this wider class and compare it to existing modularity-based methods. Our experiments show that these alternatives may outperform modularity-based methods. For example, when communities are large compared to vertex neighborhoods, a vector based on numbers of common neighbors outperforms existing community detection methods. While the focus of the present work is community detection in networks, the proposed methodology can be applied to any clustering problem where pair-wise similarity data is available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge