Good Classification Measures and How to Find Them

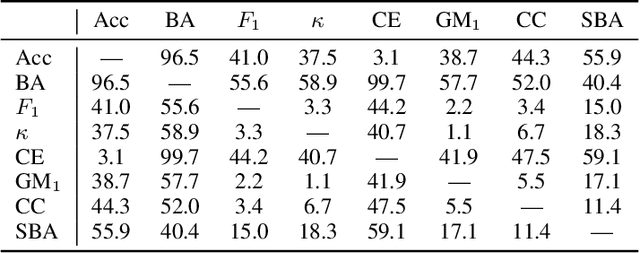
Several performance measures can be used for evaluating classification results: accuracy, F-measure, and many others. Can we say that some of them are better than others, or, ideally, choose one measure that is best in all situations? To answer this question, we conduct a systematic analysis of classification performance measures: we formally define a list of desirable properties and theoretically analyze which measures satisfy which properties. We also prove an impossibility theorem: some desirable properties cannot be simultaneously satisfied. Finally, we propose a new family of measures satisfying all desirable properties except one. This family includes the Matthews Correlation Coefficient and a so-called Symmetric Balanced Accuracy that was not previously used in classification literature. We believe that our systematic approach gives an important tool to practitioners for adequately evaluating classification results.

The Hyperspherical Geometry of Community Detection: Modularity as a Distance

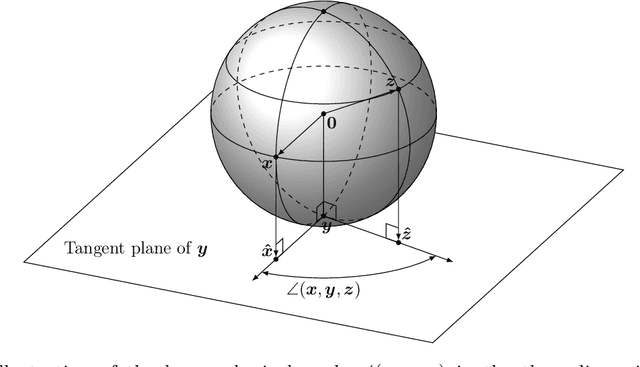
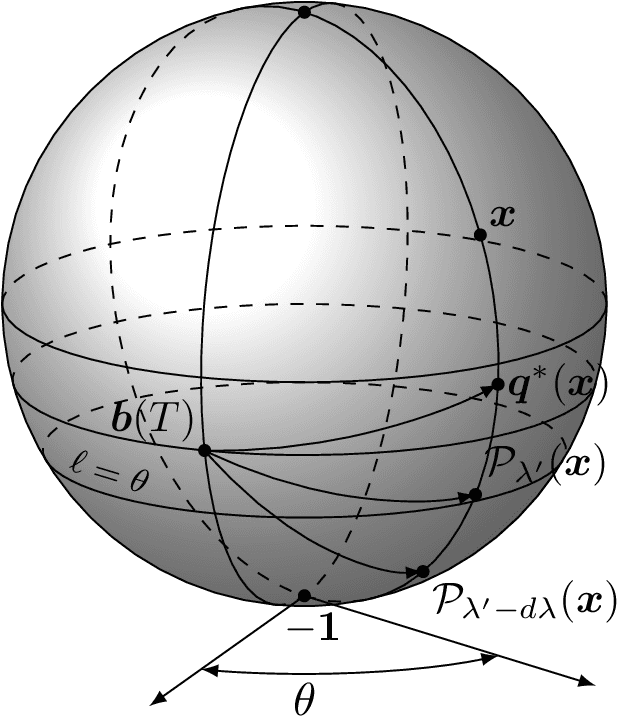
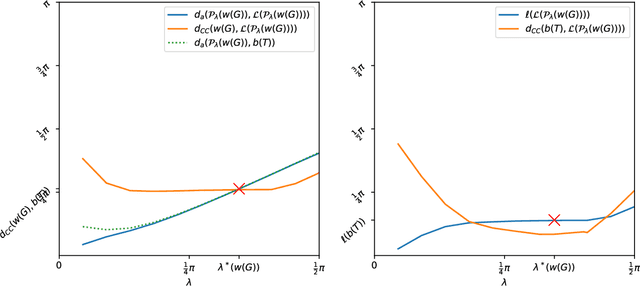
The Louvain algorithm is currently one of the most popular community detection methods. This algorithm finds communities by maximizing a quantity called modularity. In this work, we describe a metric space of clusterings, where clusterings are described by a binary vector indexed by the vertex-pairs. We extend this geometry to a hypersphere and prove that maximizing modularity is equivalent to minimizing the angular distance to some modularity vector over the set of clustering vectors. This equivalence allows us to view the Louvain algorithm as a nearest-neighbor search that approximately minimizes the distance to this modularity vector. By replacing this modularity vector by a different vector, many alternative community detection methods can be obtained. We explore this wider class and compare it to existing modularity-based methods. Our experiments show that these alternatives may outperform modularity-based methods. For example, when communities are large compared to vertex neighborhoods, a vector based on numbers of common neighbors outperforms existing community detection methods. While the focus of the present work is community detection in networks, the proposed methodology can be applied to any clustering problem where pair-wise similarity data is available.