Statistical Verification of Linear Classifiers

We propose a homogeneity test closely related to the concept of linear separability between two samples. Using the test one can answer the question whether a linear classifier is merely ``random'' or effectively captures differences between two classes. We focus on establishing upper bounds for the test's \emph{p}-value when applied to two-dimensional samples. Specifically, for normally distributed samples we experimentally demonstrate that the upper bound is highly accurate. Using this bound, we evaluate classifiers designed to detect ER-positive breast cancer recurrence based on gene pair expression. Our findings confirm significance of IGFBP6 and ELOVL5 genes in this process.

Good Classification Measures and How to Find Them

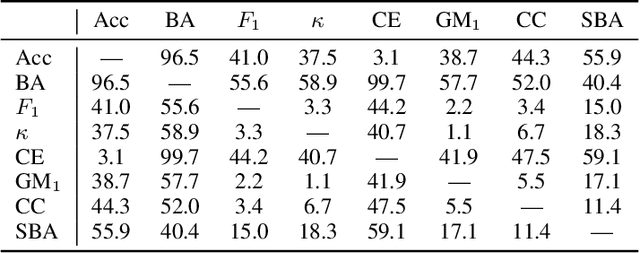
Several performance measures can be used for evaluating classification results: accuracy, F-measure, and many others. Can we say that some of them are better than others, or, ideally, choose one measure that is best in all situations? To answer this question, we conduct a systematic analysis of classification performance measures: we formally define a list of desirable properties and theoretically analyze which measures satisfy which properties. We also prove an impossibility theorem: some desirable properties cannot be simultaneously satisfied. Finally, we propose a new family of measures satisfying all desirable properties except one. This family includes the Matthews Correlation Coefficient and a so-called Symmetric Balanced Accuracy that was not previously used in classification literature. We believe that our systematic approach gives an important tool to practitioners for adequately evaluating classification results.